Поняття межі числової послідовності

Згадаймо спочатку визначення числової послідовності.

Визначення 1

Відображення безлічі натуральних чисел на множину дійсних чисел називається числовою послідовністю.

Поняття межі числової послідовності має кілька основних визначень:

• Дійсне число $a$ називається межею числової послідовності $(x_n)$, якщо для будь-якого $\varepsilon >0$ існує номер $N$, що залежить від $\varepsilon$, такий, що для будь-якого номера $n> N$ виконується нерівність $\left|x_n-a\right|
• Дійсно число $a$ називається межею числової послідовності $(x_n)$, якщо в будь-яку околицю точки $a$ потрапляють усі члени послідовності $(x_n)$, за винятком, можливо, кінцевого числа членів.

Розглянемо приклад обчислення значення межі числової послідовності:

Приклад 1

Знайти межу $(\mathop(lim)_(n\to \infty ) \frac(n^2-3n+2)(2n^2-n-1)\ )$

Рішення:

Для вирішення цього завдання спочатку нам необхідно винести за дужки старший ступінь, що входить у вираз:

$(\mathop(lim)_(n\to \infty ) \frac(n^2-3n+2)(2n^2-n-1)\ )=(\mathop(lim)_(x\to \ infty ) \frac(n^2\left(1-\frac(3)(n)+\frac(2)(n^2)\right))(n^2\left(2-\frac(1) (n)-\frac(1)(n^2)\right))\ )=(\mathop(lim)_(n\to \infty ) \frac(1-\frac(3)(n)+\ frac(2)(n^2))(2-\frac(1)(n)-\frac(1)(n^2))\ )$

Якщо в знаменнику стоїть нескінченно велика величина, то вся межа прагне до нуля, $\mathop(lim)_(n\to \infty )\frac(1)(n)=0$, використавши це, отримаємо:

$(\mathop(lim)_(n\to \infty ) \frac(1-\frac(3)(n)+\frac(2)(n^2))(2-\frac(1)(n )-\frac(1)(n^2))\ )=\frac(1-0+0)(2-0-0)=\frac(1)(2)$

Відповідь:$\frac(1)(2)$.

Поняття межі функції у точці

Поняття межі функції у точці має два класичні визначення:

Визначення терміна «межа» по Коші

Дійсно $A$ називається межею функції $f\left(x\right)$ при $x\to a$, якщо для будь-якого $\varepsilon > 0$ існує $\delta >0$, що залежить від $\varepsilon $, такий, що для будь-якого $x\in X^(\backslash a)$, що задовольняють нерівності $\left|x-a\right|

Визначення по Гейні

Дійсно $A$ називається межею функції $f\left(x\right)$ при $x\to a$, якщо для будь-якої послідовності $(x_n)\in X$, що сходить до $a$, послідовність значень $f (x_n)$ сходиться до $A$.

Ці два визначення пов'язані між собою.

Зауваження 1

Визначення межі функції по Коші та Гейні еквівалентні.

Крім класичних підходів до обчислення меж функції, пригадаємо формули, які можуть допомогти у цьому.

Таблиця еквівалентних функцій, коли $x$ нескінченно малий (прагне нуля)

Одним із підходів до вирішення меж є принцип заміни на еквівалентну функцію. Таблиця еквівалентних функцій представлена ​​нижче, щоб їй скористатися, необхідно замість функцій праворуч підставити вираз відповідну елементарну функцію зліва.

Малюнок 1. Таблиця еквівалентності функцій. Автор24 - інтернет-біржа студентських робіт

Також для вирішення меж, значення яких зводяться до невизначеності, можна застосувати правило Лопіталя. У загальному випадку невизначеність виду $\frac(0)(0)$ можна розкрити розклавши на множники чисельник і знаменник і потім скоротивши. Невизначеність, що має форму $\frac(\infty )(\infty)$ можна дозволити після поділу виразів у чисельнику і знаменника на змінну, при якій знаходиться старший ступінь.

Чудові межі

• Перша чудова межа:

$(\mathop(lim)_(x\to 0) \frac(sinx)(x)\ )=1$

• Друга чудова межа:

$\mathop(lim)_(x\to 0)((1+x))^(\frac(1)(x))=e$

Спеціальні межі

• Перша спеціальна межа:

$\mathop(lim)_(x\to 0)\frac(((log)_a (1+x-)\ ))(x)=((log)_a e\ )=\frac(1)(lna )$

• Друга спеціальна межа:

$\mathop(lim)_(x\to 0)\frac(a^x-1)(x)=lna$

• Третя спеціальна межа:

$\mathop(lim)_(x\to 0)\frac(((1+x))^(\mu )-1)(x)=\mu $

Безперервність функції

Визначення 2

Функція $f(x)$ називається безперервною в точці $x=x_0$, якщо $\forall \varepsilon >(\rm 0)$ $\exists \delta (\varepsilon ,E_(0))>(\rm 0) $ таке, що $ \ left | f (x) - f (x_ (0)) \ right |

Функція $f(x)$ безперервна в точці $х=х_0$, якщо $\mathop((\rm lim\; ))\limits_((\rm x)\to (\rm x)_((\rm 0) )) ) f(x)=f(x_(0))$.

Точка $x_0\in X$ називається точкою розриву першого роду, якщо в ній існують кінцеві межі $(\mathop(lim)_(x\to x_0-0) f(x_0)\ )$, $(\mathop(lim) _(x\to x_0+0) f(x_0)\ )$, але порушується рівність $(\mathop(lim)_(x\to x_0-0) f(x_0)\ )=(\mathop(lim)_ (x\to x_0+0) f(x_0)\ )=f(x_0)$

Причому, якщо $(\mathop(lim)_(x\to x_0-0) f(x_0)\ )=(\mathop(lim)_(x\to x_0+0) f(x_0)\ )\ne f (x_0)$, то це точка усуненого розриву, а якщо $(\mathop(lim)_(x\to x_0-0) f(x_0)\ )\ne (\mathop(lim)_(x\to x_0+ 0) f(x_0)\ )$, то точка стрибка функції.

Точка $x_0\in X$ називається точкою розриву другого роду, якщо в ній хоча б одна з меж $(\mathop(lim)_(x\to x_0-0) f(x_0)\ )$, $(\mathop( lim)_(x\to x_0+0) f(x_0)\ )$ являє собою нескінченність або не існує.

Приклад 2

Дослідити безперервність $y=\frac(2)(x)$

Рішення:

$(\mathop(lim)_(x\to 0-0) f(x)\ )=(\mathop(lim)_(x\to 0-0) \frac(2)(x)\ )=- \infty$ - функція має точку розриву другого роду.

Безперервність функції. Крапки розриву.

Іде бичок, хитається, зітхає на ходу:
- Ох, дошка кінчається, зараз я впаду!

На даному уроці ми розберемо поняття безперервності функції, класифікацію точок розриву та поширене практичне завдання дослідження функції на безперервність. Із самої назви теми багато хто інтуїтивно здогадується, про що піде мова, і думають, що матеріал досить простий. Це правда. Але саме нескладні завдання найчастіше карають за зневагу та поверхневий підхід до їх вирішення. Тому рекомендую дуже уважно вивчити статтю та вловити всі тонкощі та технічні прийоми.

Що потрібно знати та вміти?Не дуже багато. Для якісного засвоєння уроку необхідно розуміти, що таке межа функції. Читачам з низьким рівнем підготовки достатньо осмислити статтю Межі функцій. Приклади рішеньі подивитися геометричний зміст межі в методичці Графіки та властивості елементарних функцій. Також бажано ознайомитись з геометричними перетвореннями графіків, Оскільки практика здебільшого передбачає побудову креслення. Перспективи оптимістичні для всіх, і навіть повний чайник зуміє самостійно впоратися із завданням у найближчу годину-другу!

Безперервність функції. Точки розриву та їх класифікація

Поняття безперервності функції

Розглянемо деяку функцію, безперервну на всій числовій прямій:

Або, кажучи лаконічніше, наша функція безперервна на (множині дійсних чисел).

Який «обивацький» критерій безперервності? Очевидно, графік безперервної функції можна накреслити, не відриваючи олівця від паперу.

При цьому слід чітко відрізняти два прості поняття: область визначення функціїі безперервність функції. У загальному випадку Це не одне і те ж. Наприклад:

Ця функція визначена на всій числовій прямій, тобто для кожногозначення "ікс" існує своє значення "гравця". Зокрема, якщо , то . Зауважте, що інша точка виколота, адже за визначенням функції, значенням аргументу має відповідати єдинезначення функції. Таким чином, область визначенняНашої функції: .

Однак ця функція не є безперервною на !Цілком очевидно, що в точці вона терпить розрив. Термін теж цілком зрозумілий і наочний, дійсно, олівець тут по-кожному доведеться відірвати від паперу. Трохи згодом ми розглянемо класифікацію точок розриву.

Безперервність функції в точці та на інтервалі

У тій чи іншій математичній задачі мова може йти про безперервність функції в точці, безперервність функції на інтервалі, напівінтервалі або безперервність функції на відрізку. Тобто, не існує «просто безперервності»– функція може бути безперервною десь. І основним «цеглиною» всього іншого є безперервність функції у точці .

Теорія математичного аналізу дає визначення безперервності функції у точці з допомогою «дельта» і «эпсилон» околиць, але практично у ході інше визначення, якому ми й приділимо найпильнішу увагу.

Спочатку згадаємо односторонні межі, що увірвалися в наше життя на першому уроці про графіки функцій. Розглянемо буденну ситуацію:

Якщо наближатися по осі до точки зліва(червона стрілка), то відповідні значення "ігреків" будуть йти по осі до точки (малінова стрілка). Математично цей факт фіксується за допомогою лівосторонньої межі:

Зверніть увагу на запис (читається «ікс прагне до зліва»). "Добавка" "мінус нуль" символізує , По суті це і позначає, що ми підходимо до числа з лівого боку.

Аналогічно, якщо наближатися до точки «ка» справа(синя стрілка), то «ігреки» прийдуть до того ж значення, але вже за зеленою стрілкою, і правостороння межаоформиться так:

Добавка символізує , і запис читається так: «ікс прагне до як праворуч».

Якщо односторонні межі кінцеві та рівні(як у нашому випадку): , то будемо говорити, що існує Загальна межа . Все просто, спільна межа – це наша «звичайна» межа функції, рівний кінцевому числу.

Зауважте, що якщо функція не визначена при (виколіть чорну точку на гілці графіка), перераховані викладки залишаються справедливими. Як уже неодноразово наголошувалося, зокрема, у статті про нескінченно малі функції, вирази означають, що «ікс» нескінченно близьконаближається до точки, при цьому НЕ МАЄ ЗНАЧЕННЯ, чи визначена сама функція у цій точці чи ні. Хороший приклад зустрінеться у наступному параграфі, коли аналізу піддасться функція .

Визначення: функція безперервна у точці , якщо межа функції у цій точці дорівнює значенню функції у цій точке: .

Визначення деталізується за таких умов:

1) Функція має бути визначена в точці, тобто має існувати значення.

2) Повинна існувати загальна межа функції. Як зазначалося вище, це передбачає існування та рівність односторонніх меж: .

3) Межа функції у цій точці має дорівнювати значенню функції у цій точці: .

Якщо порушено хоча б однеіз трьох умов, то функція втрачає властивість безперервності в точці .

Безперервність функції на інтерваліформулюється дотепно і дуже просто: функція безперервна на інтервалі, якщо вона безперервна в кожній точці цього інтервалу.

Зокрема, багато функцій безперервні на нескінченному інтервалі, тобто на безлічі дійсних чисел. Це лінійна функція, багаточлени, експонента, синус, косинус та ін. І взагалі будь-яка елементарна функціябезперервна на своїй області визначення, наприклад, логарифмічна функція безперервна на інтервалі . Сподіваюся, на даний момент ви досить добре уявляєте, як виглядають графіки основних функцій. Більш детальну інформацію про їх безперервність можна отримати у доброї людини на прізвище Фіхтенгольц.

З безперервністю функції на відрізку і напівінтервала теж все нескладно, але про це доречніше розповісти на уроці про знаходження мінімального та максимального значень функції на відрізку, а поки що голову забивати не будемо.

Класифікація точок розриву

Цікаве життя функцій багата будь-якими особливими точками, і точки розриву лише одна зі сторінок їх біографії.

Примітка : про всяк випадок зупинюся на елементарному моменті: точка розриву – це завжди окремо взята точка– не буває «кілька точок розриву поспіль», тобто немає такого поняття, як «інтервал розривів».

Дані точки у свою чергу поділяються на дві великі групи: розриви першого родуі розриви другого роду. Кожен тип розриву має свої характерні особливості, які ми розглянемо прямо зараз:

Точка розриву першого роду

Якщо у точці порушено умову безперервності та односторонні межі кінцеві , то вона називається точкою розриву першого роду.

Почнемо з найоптимістичнішого випадку. За початковим задумом уроку я хотів розповісти теорію «загалом», але щоб продемонструвати реальність матеріалу, зупинився на варіанті з конкретними дійовими особами.

Похмуро, як фото молодят на тлі Вічного вогню, але нижченаведений кадр загальноприйнятий. Зобразимо на кресленні графік функції:


Ця функція безперервна на всій числовій прямій, крім точки . І справді, знаменник же не може дорівнювати нулю. Проте відповідно до змісту межі – ми можемо нескінченно близьконаближатися до «нуля» і ліворуч і праворуч, тобто односторонні межі існують і, очевидно, збігаються:
(Умова №2 безперервності виконана).

Але функція не визначена в точці, отже, порушено Умову №1 безперервності, і функція зазнає розриву в цій точці.

Розрив такого виду (з існуючим загальною межею) називають усувним розривом. Чому усувається? Тому що функцію можна довизначитиу точці розриву:

Дивно виглядає? Можливо. Але такий запис функції нічого не суперечить! Тепер розрив усунений і всі щасливі:


Виконаємо формальну перевірку:

2) – загальна межа існує;
3)

Таким чином, всі три умови виконані, і функція безперервна в точці визначення безперервності функції в точці.

Втім, ненависники матану можуть визначити функцію поганим способом, наприклад :


Цікаво, що тут виконано перші дві умови безперервності:
1) – функція визначена у цій точці;
2) - Спільна межа існує.

Але третій рубіж не пройдено: тобто межа функції в точці не дорівнюєзначення цієї функції в даній точці.

Таким чином, у точці функція зазнає розриву.

Другий, сумніший випадок носить назву розриву першого роду зі стрибком. А смуток навіюють односторонні межі, які кінцеві та різні. Приклад зображений на другому кресленні уроку. Такий розрив виникає, як правило, у шматково-заданих функціях, про які вже згадувалося у статті про перетворення графіків.

Розглянемо шматочкову функцію і виконаємо її креслення. Як збудувати графік? Дуже просто. На напівінтервалі креслимо фрагмент параболи (зелений колір), на інтервалі – відрізок прямий (червоний колір) та на напівінтервалі – пряму (синій колір).

При цьому через нерівність значення визначено для квадратичної функції (зелена точка), і через нерівність , значення визначено для лінійної функції (синя точка):

У найважчому випадку слід вдатися до поточкового побудови кожного шматка графіка (див. перший урок про графіки функцій).

Зараз нас цікавитиме лише точка. Досліджуємо її на безперервність:

2) Обчислимо односторонні межі.

Зліва у нас червоний відрізок прямий, тому лівостороння межа:

Праворуч – синя пряма, та правостороння межа:

В результаті отримано кінцеві числа, причому вони не рівні. Оскільки односторонні межі кінцеві та різні: , то наша функція терпить розрив першого роду зі стрибком.

Логічно, що розрив не усунемо – функцію дійсно не довизначити і «не склеїти», як у попередньому прикладі.

Точки розриву другого роду

Зазвичай до цієї категорії хитро відносять решту випадків розриву. Все перераховувати не буду, оскільки на практиці в 99% відсотках завдань вам зустрінеться нескінченний розрив– коли лівосторонній чи правосторонній, а частіше, обидві межі нескінченні.

І, звичайно ж, картинка, що напрошується, - гіпербола в точці нуль. Тут обидві односторонні межі нескінченні: , Отже, функція зазнає розриву другого роду в точці .

Я намагаюся наповнювати свої статті максимально різноманітним змістом, тому давайте подивимося на графік функції, який ще не зустрічався:

за стандартною схемою:

1) Функція не визначена у цій точці, оскільки знаменник перетворюється на нуль.

Звичайно, можна відразу зробити висновок про те, що функція зазнає розриву точки, але добре б класифікувати характер розриву, що часто потрібно за умовою. Для цього:

Нагадую, що під записом розуміється нескінченно мале негативне число, а під записом – нескінченно мале позитивне число.

Односторонні межі нескінченні, отже, функція зазнає розриву 2-го роду в точці . Вісь ординат є вертикальною асимптотоюдля графіка.

Не рідкісна ситуація, коли обидві односторонні межі існують, але нескінченний лише один із них, наприклад:

Це графік функції.

Досліджуємо на безперервність точку:

1) Функція не визначена у цій точці.

2) Обчислимо односторонні межі: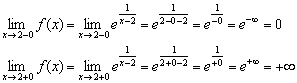

Про методику обчислення таких односторонніх меж поговоримо у двох останніх прикладах лекції, хоча багато читачів усе вже побачили та здогадалися.

Лівостороння межа кінцева і дорівнює нулю (у саму точку ми «не заходимо»), але правостороння межа нескінченна і помаранчева гілка графіка нескінченно близько наближається до своєї вертикальній асимптоті, Заданою рівнянням (чорний пунктир).

Таким чином, функція терпить розрив другого родуу точці.

Як і для розриву одного роду, у самій точці розриву функція може бути визначена. Наприклад, для шматкової функції сміливо ставимо чорну жирну крапку на початку координат. Справа ж - гілка гіперболи, і правостороння межа нескінченна. Думаю, майже всі уявили, як виглядає цей графік.

Те, чого всі з нетерпінням чекали:

Як вивчити функцію на безперервність?

Дослідження функції на безперервність у точці проводиться за вже накатаною рутинною схемою, яка полягає у перевірці трьох умов безперервності:

Приклад 1

Дослідити функцію

Рішення:

1) Під приціл потрапляє єдина точка , де функція не визначена.

2) Обчислимо односторонні межі:

Односторонні межі кінцеві та рівні.

Таким чином, у точці функція терпить усунутий розрив.

Як виглядає графік цієї функції?

Хочеться провести спрощення , і начебто виходить звичайна парабола. АЛЕвихідна функція не визначена в точці, тому обов'язкове наступне застереження:

Виконаємо креслення:

Відповідь: функція безперервна на всій числовій прямій крім точки , в якій вона терпить розрив.

Функцію можна визначити хорошим або не дуже способом, але за умовою цього не потрібно.

Ви скажете, приклад надуманий? Анітрохи. Десятки разів зустрічалося практично. Майже всі завдання сайту родом із реальних самостійних та контрольних робіт.

Розробимося з улюбленими модулями:

Приклад 2

Дослідити функцію на безперервність. Визначити характер розривів функції, якщо вони існують. Виконати креслення.

Рішення: чомусь студенти бояться і не люблять функції з модулем, хоча нічого складного в них немає Таких речей ми вже трохи торкнулися на уроці Геометричні перетворення графіків. Оскільки модуль невід'ємний, він розкривається так: , де "альфа" - деякий вираз. В даному випадку , і наша функція повинна розписатися кусковим чином: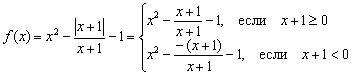

Але дроби обох шматків доведеться скоротити на . Скорочення, як і в попередньому прикладі, не пройде без наслідків. Вихідна функція не визначена в точці , оскільки знаменник перетворюється на нуль. Тому в системі слід додатково вказати умову і першу нерівність зробити суворим:

Тепер про ДУЖЕ КОРИСНИЙ прийом рішення: перед чистовим оформленням завдання на чернетці вигідно зробити креслення (незалежно від того, потрібен він за умовою чи ні). Це допоможе, по-перше, відразу побачити точки безперервності і точки розриву, а, по-друге, 100% убереже від помилок при знаходженні односторонніх меж.

Виконаємо креслення. Відповідно до наших викладок, зліва від точки необхідно накреслити фрагмент параболи (синій колір), а праворуч – шматок параболи (червоний колір), при цьому функція не визначена в самій точці:

Якщо є сумніви, візьміть декілька значень "ікс", підставте їх у функцію (не забуваючи, що модуль знищує можливий знак мінус) і звіртеся з графіком.

Досліджуємо функцію на безперервність аналітично:

1) Функція не визначена в точці , тому відразу можна сказати, що не є в ній безперервною.

2) Встановимо характер розриву, при цьому обчислимо односторонні межі:

Односторонні межі кінцеві і різні, отже, функція зазнає розриву 1-го роду зі стрибком у точці . Ще раз зауважте, що при знаходженні меж немає значення, визначена функція в точці розриву чи ні.

Тепер залишається перенести креслення з чернетки (він зроблений як би за допомогою дослідження;-)) і завершити завдання:

Відповідь: функція безперервна на всій числовій прямій крім точки, в якій вона зазнає розриву першого роду зі стрибком.

Іноді вимагають додатково вказати стрибок розриву. Обчислюється він елементарно – з правої межі треба відняти ліву межу: , тобто у точці розриву наша функція стрибнула на 2 одиниці вниз (що нам повідомляє знак «мінус»).

Приклад 3

Дослідити функцію на безперервність. Визначити характер розривів функції, якщо вони існують. Зробити креслення.

Це приклад самостійного рішення, приблизний зразок рішення наприкінці уроку.

Перейдемо до найбільш популярної та поширеної версії завдання, коли функція складається з трьох шматків:

Приклад 4

Дослідити функцію на безперервність та побудувати графік функції .

Рішення: очевидно, що всі три частини функції безперервні на відповідних інтервалах, тому залишилося перевірити лише дві точки «стику» між шматками. Спочатку виконаємо креслення на чернетці, техніку побудови я досить докладно закоментував у першій частині статті. Єдине, необхідно акуратно простежити за нашими особливими точками: через нерівність значення належить прямий (зелена точка), і через нерівність значення належить параболі (червона точка):


Ну ось, у принципі, все зрозуміло =) Залишилось оформити рішення. Для кожної з двох «стикових» точок стандартно перевіряємо 3 умови безперервності:

I)Досліджуємо на безперервність точку

1)

Односторонні межі кінцеві і різні, отже, функція зазнає розриву 1-го роду зі стрибком у точці .

Обчислимо стрибок розриву як різницю правої та лівої меж:
тобто графік рвонув на одну одиницю вгору.

II)Досліджуємо на безперервність точку

1) – функція визначена у цій точці.

2) Знайдемо односторонні межі:

– односторонні межі кінцеві і рівні, отже, існує спільна межа.

3) – межа функції у точці дорівнює значенню цієї функції у цій точці.

На завершальному етапі переносимо креслення на чистовик, після чого ставимо фінальний акорд:

Відповідь: функція безперервна на всій числовій прямій, крім точки, в якій вона зазнає розриву першого роду зі стрибком.

Приклад 5

Дослідити функцію на безперервність та побудувати її графік .

Це приклад для самостійного розв'язання, коротке рішення та приблизний зразок оформлення завдання наприкінці уроку.

Може скластися враження, що в одній точці функція обов'язково має бути безперервною, а в іншій – обов'язково має бути розрив. Насправді це далеко не завжди так. Постарайтеся не нехтувати прикладами, що залишилися - буде кілька цікавих і важливих фішок:

Приклад 6

Дана функція . Дослідити функцію на безперервність у точках. Побудувати графік.

Рішення: і знову відразу виконаємо креслення на чернетці:

Особливість даного графіка у тому, що з кускова функція задається рівнянням осі абсцис . Тут ця ділянка промальована зеленим кольором, а в зошит її зазвичай жирно виділяють простим олівцем. І, звичайно ж, не забуваємо про наших баранів: значення відноситься до гілки тангенса (червона точка), а значення належить прямій.

З креслення все зрозуміло - функція безперервна по всій числовій прямій, залишилося оформити рішення, яке доводиться до повного автоматизму буквально після 3-4 подібних прикладів:

I)Досліджуємо на безперервність точку

1) – функція визначено у цій точці.

2) Обчислимо односторонні межі:

, Отже, спільна межа існує.

На всякий пожежник нагадаю тривіальний факт: межа константи дорівнює самій константі. У цьому випадку межа нуля дорівнює самому нулю (лівостороння межа).

3) – межа функції у точці дорівнює значенню цієї функції у цій точці.

Таким чином, функція безперервна в точці визначення безперервності функції в точці.

II)Досліджуємо на безперервність точку

1) – функція визначено у цій точці.

2) Знайдемо односторонні межі:

І тут – межа одиниці дорівнює самій одиниці.

- Спільна межа існує.

3) – межа функції у точці дорівнює значенню цієї функції у цій точці.

Таким чином, функція безперервна в точці визначення безперервності функції в точці.

Як завжди, після дослідження переносимо наш креслення на чистовик.

Відповідь: функція безперервна в точках.

Зверніть увагу, що за умови нас нічого не питали про дослідження всієї функції на безперервність, і хорошим математичним тоном вважається формулювати точний та чіткийвідповідь на поставлене запитання. До речі, якщо за умовою не потрібно будувати графік, ви маєте повне право його і не будувати (правда, потім викладач може змусити це зробити).

Невелика математична «скоромовка» для самостійного вирішення:

Приклад 7

Дана функція . Дослідити функцію на безперервність у точках. Класифікувати точки розриву, якщо вони є. Виконати креслення.

Постарайтеся правильно "вимовити" всі "слова" =) І графік намалювати точніше, точність, вона скрізь зайвою не буде;-)

Як ви пам'ятаєте, я рекомендував негайно виконувати креслення на чернетці, але іноді трапляються такі приклади, де не відразу зрозумієш, як виглядає графік. Тому у ряді випадків вигідно спочатку знайти односторонні межі і лише потім на основі дослідження зобразити гілки. У двох заключних прикладах ми, крім того, освоїмо техніку обчислення деяких односторонніх меж:

Приклад 8

Дослідити на безперервність функцію та побудувати її схематичний графік.

Рішення: Негативні точки очевидні: (звертає в нуль знаменник показника) і (звертає в нуль знаменник всього дробу). Зрозуміло, як виглядає графік цієї функції, отже, спочатку краще провести дослідження.

Межа і безперервність

функції однієї змінної

3.1.1. Визначення. Число А xтим, хто прагне x 0 якщо для будь-якого числа
знайдеться число
(
), і виконуватиметься умова:

якщо
, то
.

(Символіка:
).

Якщо точки графіка Гфункції

, коли необмежено близько наближається до точки (Тобто.
), (див. рис. 3.1), то ця обставина є геометричним еквівалентом того, що функція
при
має граничне значення (межа) A(Символіка:
).

Графік функції ,

Мал. 3.1

Слід зазначити, що у визначенні граничного значення (межі) функції при xщо прагне до x 0 нічого не говориться про поведінку функції в точці x 0 . У самій точці x 0 функція може бути не визначена, можливо
, а може бути
.

Якщо
, то функція називається нескінченно малою при
.

Проміжок називають  - околицею точки x 0 з виколотим центром. Використовуючи цю назву, можна сказати так: якщо для будь-якого числа знайдеться число і буде виконуватися умова: якщо
, то
.

3.1.2. Визначення. , якщо для будь-якої сходиться до x 0 послідовності
послідовність
сходиться до А.

3.1.3. Доведемо еквівалентність визначень розділів 3.1.1 та 3.1.2

Нехай спочатку в сенсі першого визначення та нехай
(
), тоді все крім їх кінцевого числа задовольняють нерівності
, де  вибрано за  у сенсі першого визначення, тобто.
, тобто. з першого визначення випливає друге. Нехай тепер
у сенсі другого визначення та припустимо, що у сенсі другого визначення
, тобто. для деякого при будь-яких малих (наприклад, при
) знайшлася послідовність
, але при цьому
. Прийшли до протиріччя, отже, з другого визначення випливає перше.

3.1.4. Еквівалентність цих визначень особливо зручна, бо всі доведені раніше теореми про властивості меж для послідовностей переносяться майже автоматично новий випадок. Слід лише уточнити поняття обмеженості. Відповідна теорема має таке формулювання:

Якщо
, то обмежена на деякій  - околиці точки x 0 з виколотим центром.

3.2.1.Теорема. Нехай
,
,

тоді,
,

,

.

3.2.2. Нехай

- довільна, що сходить до x 0 послідовність значень аргументів функцій та
. Відповідні послідовності
і
значень цих функцій мають межі Aі B. Але тоді, через теорему розділу 2.13.2, послідовності
,
і
мають межі, відповідно рівні A +B,
і
. Відповідно до визначення межі функції у точці (див. розділ 2.5.2) це означає, що

,
,

.

3.2.3. Теорема. Якщо
,
, і в деякій околиці

має місце

.

3.2.4. За визначенням межі функції в точці x 0 для будь-якої послідовності
такий, що

послідовність значень функції має межу рівну А. Це означає, що для будь-кого
існує номер
виконується. Аналогічно для послідовності
існує номер
такий, що для будь-якого номера
виконується. Вибираючи
, отримуємо, що для всіх
виконується. З цього ланцюжка нерівностей маємо для будь-якого, що означає, що
.

3.2.5. Визначення. Число Аназивається граничним значенням (межею) функції при xтим, хто прагне x 0 праворуч (символіка:
), якщо для будь-якого числа знайдеться число () і виконуватиметься умова: якщо
, то
.

Безліч називають правою  - околицею точки x 0 . Аналогічно визначається поняття граничного значення (межі) зліва (
).

3.2.6. Теорема. Функція має граничне значення (межа) рівний Атоді і лише тоді, коли

,

3.3.1. Визначення. Число Аназивається граничним значенням (межею) функції при xтим, хто прагне нескінченності, якщо для будь-якого числа знайдеться число
(
) і виконуватиметься умова:

якщо
, то.

(Символіка:
.)

Безліч
називається D-Навколо нескінченності.

3.3.2. Визначення. Число Аназивається граничним значенням (межею) функції при xтим, хто прагне плюс нескінченності, якщо для будь-якого числа знайдеться число D() і виконуватиметься умова:

якщо
, то.

(Символіка:
).

Якщо точки графіка Гфункції
з необмеженим зростанням
необмежено наближаються до єдиної горизонтальної прямої
(див. рис. 3.2), то ця обставина є геометричним еквівалентом того, що функція
при
має граничне значення (межа), що дорівнює числу A(Символіка:
).

Графік функції
,

Безліч
називається D-Навколо плюс нескінченності.

Аналогічно визначається поняття межі при
.

Вправи.

Сформулюйте всі теореми про межі стосовно випадків:

1)
, 2)
, 3)
, 4)
, 5)
.

3.4.1. Визначення. Функція називається нескінченно великою функцією (або просто нескінченно великою) при , якщо для будь-якого числа

, що задовольняють нерівність , виконується нерівність
.

(Символіка:
.)

Якщо виконується
, то пишуть
.

Якщо виконується
, то пишуть
.

3.4.2. Теорема. Нехай
і
при
.

Тоді
- нескінченно велика функція при .

3.4.3. Нехай довільне число. Так як - нескінченно мала функція при , то для числа
існує кількість така, що для всіх xтаких, що виконується нерівність
але тоді для тих же xвиконуються нерівність
. Тобто. - нескінченно велика функція при .

3.4.4.Теорема. Нехай - нескінченно велика функція при і за.

Тоді - нескінченно мала функція при .

(Ця теорема доводиться аналогічно до теореми розділу 3.8.2).

3.4.5. Функція
називається необмеженою при
якщо для будь-якого числа
та будь-який δ-околиці точки можна вказати точку xз цієї околиці таку, що
.

3.5.1. ВИЗНАЧЕННЯ. Функція називається безперервнийу точці , якщо
.

Остання умова можна записати і так:

.

Цей запис означає, що для безперервних функцій можна міняти місцями знак межі та знак функції

Або так: . Або знову, як на початку.

Позначимо
. Тоді
і =
і остання форма запису набуде вигляду

.

Вираз під знаком межі є збільшенням функції точки , викликане збільшенням
аргументу xу точці , що позначається зазвичай як
. У результаті отримуємо наступну форму запису умови безперервності функції у точці

,

яку називають «робочим визначенням» безперервності функції у точці.

Функція називається безперервнийу точці зліва, якщо
.

Функція називається безперервнийу точці справа, якщо
.

3.5.2. приклад.
. Ця функція безперервна для будь-кого. За допомогою теорем про властивості меж, ми відразу отримуємо: будь-яка раціональна функція безперервна у кожній точці, де вона визначена, тобто. функція виду
.

ВПРАВИ.

3.6.1. У шкільному підручнику доводиться (на високому рівні строгості), що
(Перша чудова межа). З наочних геометричних міркувань відразу виходить, що
. Зауважимо, що з лівої нерівності випливає також, що
, тобто. що функція
безперервна в нулі. Звідси вже неважко довести безперервність всіх тригонометричних функцій в усіх точках, де визначено. Справді, за
як твір нескінченно малої функції
на обмежену функцію
.

3.6.2. (2-а чудова межа). Як нам уже відомо

,

де пробігає натуральні числа. Можна показати, що
. Більш того
.

ВПРАВИ.

3.7.1. ТЕОРЕМА (про безперервність складної функції).

Якщо функція
безперервна в точці та
, а функція
безперервна в точці , то складна функція
безперервна в точці.

3.7.2. Справедливість цього твердження негайно випливає із визначення безперервності, записаного у вигляді:

3.8.1. ТЕОРЕМА. Функція безперервна в кожній точці (
).

3.8.2. Якщо вважати обґрунтованим, що функція
визначена для будь-якого і є строго монотонною (строго спадаючою при
, що строго зростає при
), то доказ не складає труднощів.

При
маємо:

тобто. при маємо
що означає, що функція безперервна при .

При
все зводиться до попереднього:

При
.

При
функція
постійна при всіх, отже, безперервна.

3.9.1. ТЕОРЕМА (про співіснування та безперервність зворотної функції).

Нехай безперервна функція суворо зменшується (строго зростає) в деякій δ - околиці точки ,
. Тоді в деякій ε - околиці точки існує зворотна функція
, яка суворо зменшується (суворо зростає) і безперервна в ε - околиці точки .

3.9.2. Доведемо тут лише безперервність зворотної функції у точці.

Візьмемо, точка yрозташована між точками
і
, отже, якщо
, то
де .

3.10.1. Отже, будь-які дозволені арифметичні дії над безперервними функціями знову призводять до безперервних функцій. Утворення їх складних і зворотних функцій не псує безперервності. Тому, з деякою часткою відповідальності, ми можемо стверджувати, що всі елементарні функції за всіх допустимих значень аргументу безперервні.

ВПРАВА.

Доведіть, що
при
(інша форма другої чудової межі).

3.11.1. Обчислення меж сильно спрощується, якщо використовувати поняття еквівалентних нескінченно малих. Поняття еквівалентності зручно узагальнити у разі довільних функцій.

Визначення. Функції і називаються еквівалентними при , якщо
(замість можна писати
,
,
,
,
).

Позначення, що використовується f ~ g.

Еквівалентність має наступні властивості

Необхідно пам'ятати наступний список еквівалентних нескінченно малих:

~
при
; (1)

~ при; (2)

~
при; (3)

~ при; (4)

~ при; (5)

~ при; (6)

~ при; (7)

~ p при; (8)

~ при
; (9)

~
при . (10)

Тут і можуть бути не незалежними змінними, а функціями
і
що прагнуть відповідно до нуля та одиниці при деякій поведінці x. Так наприклад,

~
при
,

~
при
.

Еквівалентність (1) є іншою формою запису першої чудової межі. Еквівалентності (2), (3), (6) та (7) можна довести безпосередньо. Еквівалентність (4) виходить із (1) з урахуванням властивості 2) еквівалентностей:

~
.

Аналогічно (5) та (7) виходять з (2) та (6). Справді

~
,

~
.

Еквівалентність (8) доводиться послідовним застосуванням (7) та (6):

а (9) та (10) виходять із (6) та (8) заміною
.

3.11.2. Теорема. При обчисленні меж у творі та відношенні можна змінювати функції на еквівалентні. А саме, якщо ~
, те, або обидві межі не існують одночасно, і
, або обидві ці межі немає одночасно.

Доведемо першу рівність. Нехай одна з меж, скажімо,
Існує. Тоді

.

3.11.3. Нехай (- число або символ ,
або
). Розглянемо поведінку різних б.м. функцій (так скорочуватимемо термін нескінченно мала).

ВИЗНАЧЕННЯ.
та називаються еквівалентними б.м. функціями при , якщо
(При ).

називатимемо б.м. вищого порядку, ніж б.м. функція
, якщо
(При ).

3.11.4. Якщо й еквівалентні б.м. функції, то
є б.м. функція вищого порядку ніж
і чим . - Б.М. функції при, в якій для всіх x і, якщо в цій точці функція називається точкою розриву, що усувається. має розрив другого роду. Сама точка Контрольна робота

До колоквіуму. Розділи: « Межаі безперервністьфункціїдійсною змінної» функціїоднієїзмінної», «Диференційне числення функційкількох змінних»

Тематика та приклади контрольних завдань та питань (контрольні роботи індивідуальні типові розрахунки колоквіум) i семестр контрольна робота №1 розділ «межа та безперервність функції дійсної змінної»

Контрольна робота

До колоквіуму. Розділи: « Межаі безперервністьфункціїдійсною змінної», «Диференційне числення функціїоднієїзмінної», «Диференційне числення функційкількох змінних». Числова послідовність...

Контрольна робота

До колоквіуму. Розділи: « Межаі безперервністьфункціїдійсною змінної», «Диференційне числення функціїоднієїзмінної», «Диференційне числення функційкількох змінних». Числова послідовність...

Тематика та приклади контрольних завдань та питань (контрольна робота індивідуальні типові розрахунки колоквіуми) i семестр контрольна робота розділ «межа та безперервність функції дійсної змінної»

Контрольна робота

До колоквіуму. Розділи: « Межаі безперервністьфункціїдійсною змінної», «Диференційне числення функціїоднієїзмінної», «Диференційне числення функційкількох змінних». Числова послідовність...

Лекція 19 межа та безперервність функції декількох змінних

Лекція

... Межаі безперервністьфункціїкількох змінних. 19.1. Концепція функціїкількох змінних. При розгляді функційкількох змінних... властивостям функційоднієїзмінної, безперервнихна відрізку. Див. Властивості функцій, безперервнихна...

Z (0, ±1, ±2, ±3,...) Безліч цілих чисел.Множество цілих чисел включає безліч натуральних. Q Безліч раціональних чисел. Крім цілих чисел є ще й дроби. Дроб - це вираз виду, де p - ціле число, q - натуральне. Десяткові дроби також можна записати як . Наприклад: 0,25 = 25/100 = 1/4. Цілі числа також можна записати як . Наприклад, у вигляді дробу зі знаменником "один": 2 = 2/1. Отже будь-яке раціональне число можна записати десятковим дробом - звичайно або нескінченним періодичним. R Безліч всіх дійсних чисел. Ірраціональні числа – це нескінченні неперіодичні дроби. До них відносяться: Разом дві множини (раціональних та ірраціональних чисел) - утворюють безліч дійсних (або речових) чисел.

Якщо безліч не містить жодного елемента, воно називається порожнім безліччюта записується Ø .

Квантор існування

∃- квантор існування, використовується замість слів "існує",

"є". Використовується поєднання символів ∃!, яке читається як існує єдиний.

Абсолютна величина

Визначення. Абсолютною величиною (модулем) дійсного числа називається невід'ємне число, яке визначається за формулою:

Так наприклад,

Властивості модуля

Якщо і – дійсні числа, то справедливі рівність:

Функція

залежність між двома або великою кількістю величин, при якій кожним значенням одних величин, званих аргументами функції, ставляться у відповідність значення інших величин, званих значеннями функції.

Область визначення функції

Областю визначення функції називають ті значення незалежної змінної x, у яких всі операції, які входять у функцію будуть здійснені.

Безперервна функція

Функція f (x), визначена в околиці точки a, називається безперервною в цій точці, якщо

Числові послідовності

функція виду y= f(x), xПро Nде N- множина натуральних чисел (або функція натурального аргументу), позначається y=f(n)або y 1 ,y 2 ,…, y n,…. Значення y 1 ,y 2 ,y 3 , … називають відповідно першим, другим, третім, … членами послідовності.

Межа функції безперервного аргументу

Число А називається межею функції y=f(x) при x->x0,якщо для всіх значень x, що досить мало відрізняються від числа x0, відповідні значення функції f(x) як завгодно мало відрізняється від числа A

Нескінченно мала функція

Функція y=f(x)називається нескінченно малоюпри x→aабо при x→∞, якщо або , тобто. нескінченно мала функція – це функція, межа якої у цій точці дорівнює нулю.

Топологія- Розділ математики, який займається вивченням меж і безперервністю функцій. У поєднанні з алгеброю топологія становить загальну основу математики.

Топологічний простір чи фігура –підмножина нашого однорідного евклідового простору, між точками якого задано деяке відношення близькості. Тут розглядаються постаті не як жорсткі тіла, бо як об'єкти, зроблені хіба що з дуже еластичної гуми, допускають безперервну деформацію, що зберігає їх якісні властивості.

Взаємно-однозначне безперервне відображення фігур називається гомеоморфізмом. Іншими словами, фігури гомеоморфніякщо одну можна перевести в іншу безперервною деформацією.

приклади. Гомеоморфні такі постаті (з різних груп постаті не гомеоморфні), зображені на рис. 2.

1. Відрізок та крива без самоперетинів.

2. Коло, начинка квадрата, стрічка.

3. Сфера, поверхня куба та тетраедра.

4. Коло, еліпс та завулене коло.

5. Кільце на площині (коло з діркою), кільце у просторі, двічі перекручене кільце, бічна поверхня циліндра.

6. Аркуш Мебіуса, тобто. один раз перекручене кільце, і три рази перекручене кільце.

7. Поверхня тора (бубліка), сфера з ручкою та завулений тор.

8. Сфера з двома ручками та крендель із двома дірками.

У математичному аналізі функції вивчаються шляхом меж. Змінна та межа – основні поняття.

У різних явищах деякі величини зберігають своє чисельне значення, інші змінюються. Сукупність усіх числових значень змінної величини називається областю зміни цієї змінної.

З різноманітних способів поведінки змінної величини найбільш важливим є такий, при якому змінна величина прагне до певної межі.

Постійне число aназивається межею змінної величиниxякщо абсолютна величина різниці між xі a() стає в процесі зміни змінної величини xскільки завгодно малої:

Що означає « скільки завгодно малої »? Змінна величина хпрагне до межі аЯкщо для будь-якого скільки завгодно малого (довільно малого) числа знайдеться такий момент у зміні змінної хпочинаючи з якого виконується нерівність .

Визначення межі має простий геометричний зміст: нерівність означає, що хзнаходиться в околиці точки a, тобто. в інтервалі .

Таким чином, визначення межі можна дати в геометричній формі:

Число ає межею змінної величини х, якщо для будь-якої скільки завгодно малої (довільно малої) -околиці числа аможна вказати такий момент у зміні змінної х, Починаючи з якого всі її значення потрапляють у зазначену -околицю точки а.

Зауваження. Змінна величина хможе по-різному наближатися до своєї межі: залишаючись менше цієї межі (ліворуч), більше (праворуч), коливаючись біля значення межі.

Межа послідовності

функцієюназивається закон (правило) за яким кожному елементу xдеякої множини Xвідповідає єдиний елемент yбезлічі Y.

Функція може бути задана на множині всіх натуральних чисел: . Така функція називається функцією натурального аргументуабо числовою послідовністю.

Оскільки послідовність, як і всяке безліч, не можна задати перерахуванням, вона задається загальним членом: , Де - Загальний член послідовності.

Дискретною змінною називається загальний член послідовності.

Для послідовності слова "починаючи з певного моменту" означають слова "починаючи з певного номера".

Число аназивається межею послідовності , якщо для будь-якого скільки завгодно малого (довільно малого) числа знайдеться такий номер Nщо для всіх членів послідовності з номером n>Nвиконується нерівність .

або при .

Геометрично визначення межі послідовності означає наступне: для будь-якої скільки завгодно малої (довільно малої) -околиці числа азнайдеться такий номер, що всі члени послідовності з більшими, ніж N, номерами, потрапляють у цю околицю. Поза околицею виявляється лише кінцеве число початкових членів послідовності. Натуральне число Nзалежить від : .