Selvitä diagonaalin pituus tietäen säännöllisen monikulmion sivut. Normaali monikulmio. Säännöllisen monikulmion sivujen lukumäärä

Kolmio, neliö, kuusikulmio - nämä luvut ovat melkein kaikkien tiedossa. Mutta kaukana kaikista tietää, mikä on säännöllinen monikulmio. Mutta nämä ovat kaikki samoja. Säännölliseksi monikulmioksi kutsutaan sellaista, jolla on yhtä suuret kulmat ja sivut toisiinsa nähden. Tällaisia \u200b\u200blukuja on paljon, mutta niillä kaikilla on samat ominaisuudet, ja niihin sovelletaan samoja kaavoja.

Säännöllisten monikulmioiden ominaisuudet

Jokainen säännöllinen monikulmio, olipa se sitten neliö tai kahdeksankulmainen, voidaan kirjoittaa ympyrään. Tätä perusominaisuutta käytetään usein muodon rakentamisessa. Lisäksi ympyrä voidaan kirjoittaa myös monikulmioon. Tässä tapauksessa kosketuspisteiden lukumäärä on yhtä suuri kuin sen sivujen lukumäärä. On tärkeää, että säännöllisessä monikulmiossa olevalla ympyrällä on yhteinen keskipiste sen kanssa. Näihin geometrisiin hahmoihin kohdistetaan yksi lause. Säännöllisen n-gonin mikä tahansa sivu on kytketty sen lähellä kuvatun ympyrän säteeseen R. Siksi se voidaan laskea seuraavan kaavan avulla: а \u003d 2R ∙ sin180 °. Kautta voit löytää paitsi sivut, mutta myös monikulmion kehä.

Kuinka löytää normaalin monikulmion sivujen lukumäärä

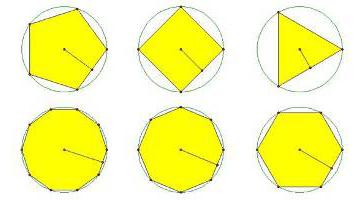Jokainen koostuu useista keskenään samanlaisista segmenteistä, jotka muodostaessaan yhteyden muodostavat suljetun viivan. Lisäksi kaikilla tuloksena olevan kuvan kulmilla on sama arvo. Polygons jaetaan yksinkertaisiin ja monimutkaisiin. Ensimmäinen ryhmä sisältää kolmion ja neliön. Monimutkaisissa monikulmioissa on suurempi määrä sivuja. Ne sisältävät myös tähtiä. Monimutkaisten säännöllisten monikulmioiden sivut löytyvät kirjoittamalla ne ympyrään. Annamme todistuksen. Piirrä säännöllinen monikulmio, jossa on mielivaltainen määrä sivuja n. Kuvaile ympyrä sen ympärillä. Määritä säde R. Nyt kuvittele, että annetaan jokin n-gon. Jos sen kulmien pisteet sijaitsevat ympyrällä ja ovat keskenään yhtä suuret, niin sivut voidaan löytää kaavalla: a \u003d 2R ∙ sinα: 2.

Löydät kirjoitetun säännöllisen kolmion sivujen lukumäärän

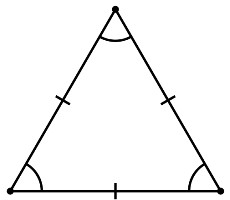
Tasasivuinen kolmio on säännöllinen monikulmio. Kaavoja sovelletaan siihen samoin kuin neliöön ja n-goniin. Kolmion katsotaan olevan oikein, jos sen pituudet ovat samat. Kulmat ovat 60ны. Rakennamme kolmion, jolla on tietty pituus sivuja a. Kun tiedät sen mediaanin ja korkeuden, löydät sen sivujen merkityksen. Tätä varten käytämme menetelmää kaavan a \u003d x: cosα löytämiseksi, missä x on mediaani tai korkeus. Koska kolmion kaikki sivut ovat yhtä suuret, saadaan a \u003d b \u003d c. Seuraava lause on totta: a \u003d b \u003d c \u003d x: cosα. Samoin voit löytää sivujen arvon nelikulmaisesta kolmiosta, mutta x on annettu korkeus. Tässä tapauksessa se tulisi työntää tiukasti kuvan pohjaan. Joten, tietäen korkeuden x, löydämme tasakulmaisen kolmion sivun a kaavalla a \u003d b \u003d x: cosα. A-arvon löytämisen jälkeen voidaan laskea kannan c pituus. Käytämme Pythagoran lausetta. Etsitään puolikkaan arvon c arvoa: 2 \u003d √ (x: cosα) ^ 2 - (x ^ 2) \u003d √x ^ 2 (1 - cos ^ 2α): cos ^ 2α \u003d x ∙ tgα. Sitten c \u003d 2xtgα. Näin yksinkertaisella tavalla löydät minkä tahansa kirjoitetun monikulmion sivujen lukumäärän.

Ympyrään merkityn neliön sivujen laskeminen

Kuten muissakin kirjoitetuissa säännöllisissä monikulmioissa, neliöllä on yhtä suuret sivut ja kulmat. Siihen sovelletaan samoja kaavoja kuin kolmioon. Neliön sivut voidaan laskea diagonaaliarvon avulla. Tarkastele tätä menetelmää yksityiskohtaisemmin. Tiedetään, että diagonaali jakaa kulman puoliksi. Aluksi sen arvo oli 90 astetta. Siten jakamisen jälkeen niiden kaksi kulmaa, jotka on muodostettu pohjaan, ovat yhtä suuret kuin 45 astetta. Siksi neliön molemmat sivut ovat yhtä suuret, toisin sanoen: a \u003d b \u003d c \u003d d \u003d e ∙ cosα \u003d e√2: 2, missä e on neliön diagonaali tai oikean kolmion jakamisen jälkeen muodostettu pohja. Tämä ei ole ainoa tapa löytää neliön reunat. Täytä tämä muoto ympyrään. Tietäen tämän ympyrän säteen R, löydämme neliön sivun. Laskemme sen seuraavasti: a4 \u003d R√2. Säännöllisten monikulmioiden säteet lasketaan kaavalla R \u003d a: 2tg (360 o: 2n), missä a on sivun pituus.

Kuinka laskea n-gonin kehä

N-gonin kehä on kaikkien sen puolien summa. Sitä ei ole vaikea laskea. Tätä varten sinun on tunnettava kaikkien osapuolten arvot. Joillekin monikulmityypeille on olemassa erityisiä kaavoja. Niiden avulla löydät kehän paljon nopeammin. Tiedetään, että millä tahansa säännöllisellä monikulmimella on yhtä suuret puolet. Siksi sen kehän laskemiseksi riittää, että tiedät ainakin yhden niistä. Kaava riippuu kuvan sivujen lukumäärästä. Yleensä se näyttää tältä: P \u003d an, missä a on sivun arvo ja n on kulmien lukumäärä. Esimerkiksi, jos haluat löytää säännöllisen kahdeksankulman, jonka reuna on 3 cm, kehän, se on kerrottava 8: lla, ts. P \u003d 3 ∙ 8 \u003d 24 cm. Kuusikulmion, jonka sivu on 5 cm, laske tämä: P \u003d 5 ∙ 6 \u003d 30 cm. Ja niin jokainen monikulmio.

Löydä suuntakuvan, neliön ja rombun kehä

Riippuen siitä, kuinka monta sivua säännöllisellä monikulmioilla on, sen kehä lasketaan. Tämä helpottaa suuresti tehtävää. Itse asiassa toisin kuin muut hahmot, tässä tapauksessa ei tarvitse etsiä kaikkia sen puolia, vain yhtä. Samalla periaatteella löydämme nelikulmien kehän, toisin sanoen neliön ja rombin. Huolimatta siitä, että nämä ovat erilaisia \u200b\u200blukuja, niiden kaava on yksi P \u003d 4a, missä a on sivu. Annamme esimerkin. Jos rombin tai neliön sivu on 6 cm, löydämme kehän seuraavasti: P \u003d 4 ∙ 6 \u003d 24 cm. Suorakuvassa vain vastakkaiset sivut ovat yhtä suuret. Siksi sen kehä löytyy toisella menetelmällä. Joten meidän on tiedettävä lukujen pituus ja leveys. Sovelletaan sitten kaavaa P \u003d (a + c) ∙ 2. Suorakuvaa, jossa kaikki sivut ovat yhtä suuret ja niiden välisiä kulmia kutsutaan rombiksi.

Tasasivuisen ja suorakulmaisen kolmion kehän löytäminen

Oikean kehä löytyy kaavasta P \u003d 3a, missä a on sivun pituus. Jos hänet ei tunneta, hänet voidaan löytää mediaanin kautta. Oikeassa kolmiossa vain kaksi puolta ovat yhtä tärkeitä. Pohja löytyy Pythagoran lauseen kautta. Kun kaikkien kolmen osapuolen arvot ovat tiedossa, laskemme kehän. Se voidaan löytää kaavalla P \u003d a + b + c, jossa a ja b ovat yhtä suuret puolet ja c on emäs. Muista, että tasakulmaisessa kolmiossa a \u003d b \u003d a, mikä tarkoittaa, että a + b \u003d 2a, sitten P \u003d 2a + c. Esimerkiksi, nelikulmaisen kolmion sivu on 4 cm, löydämme sen kannan ja kehän. Laskemme hypoteenuksen arvon Pythagoraan lauseella \u003d √а 2 + в 2 \u003d √16 + 16 \u003d √32 \u003d 5,65 cm. Nyt lasketaan kehä P \u003d 2 ∙ 4 + 5,65 \u003d 13,65 cm.

Kuinka löytää normaalin monikulmion kulmat

Säännöllinen monikulmio löytyy elämästämme joka päivä, esimerkiksi tavallinen neliö, kolmio, kahdeksankulmainen. Vaikuttaa siltä, \u200b\u200bettei ole mitään helpompaa kuin rakentaa tämä hahmo itse. Mutta tämä on vain vain ensi silmäyksellä. Minkä tahansa n-gonin rakentamiseksi on välttämätöntä tietää sen kulmien arvo. Mutta miten löytää ne? Jopa antiikin tutkijat yrittivät rakentaa säännöllisiä monikulmioita. He arvasivat sopivan heidät ympyrään. Ja sitten tarvittavat kohdat merkittiin siihen, yhdistettiin suorilla viivoilla. Yksinkertaisten lukujen tapauksessa rakennusongelma ratkaistiin. Saatiin kaavat ja lauseet. Esimerkiksi Euclid kuuluisassa teoksessaan "Alku" osallistui 3-, 4-, 5-, 6- ja 15-hajojen ongelmien ratkaisemiseen. Hän löysi tapoja rakentaa ne ja löytää kulmat. Mieti, miten tämä tehdään 15-gon: lle. Ensin on laskettava sen sisäisten kulmien summa. On välttämätöntä käyttää kaavaa S \u003d 180⁰ (n-2). Joten, meille annetaan 15-gon, joten luku n on 15. Korvaa tiedossa olevat tiedot kaavaan ja saada S \u003d 180⁰ (15 - 2) \u003d 180⁰ x 13 \u003d 2340⁰. Löysimme kaikkien 15-gonin kaikkien sisäkulmien summan. Nyt sinun on saatava arvo jokaiselle niistä. Kulmia on yhteensä 15. Lasketaan 2340⁰: 15 \u003d 156⁰. Joten jokainen sisäinen kulma on 156⁰, nyt voit rakentaa viivaimen ja kompassin avulla säännöllisen 15-gon. Entä entistä monimutkaisemmat n-gonit? Useiden vuosisatojen ajan tutkijat ovat kamppailleet tämän ongelman ratkaisemiseksi. Se löysi vasta 1700-luvulla Karl Friedrich Gauss. Hän pystyi rakentamaan 65537-gon. Siitä lähtien ongelman on katsottu olevan virallisesti täysin ratkaistu.

N-gonien kulmien laskeminen radiaaneina

Tietenkin on olemassa useita tapoja löytää monikulmioiden kulmat. Useimmiten ne lasketaan asteina. Mutta voit ilmaista ne radiaaneina. Kuinka tehdä se? On tarpeen toimia seuraavasti. Ensin selvitetään säännöllisen monikulmion sivujen lukumäärä ja vähennetään siitä 2. Joten saadaan arvo: n - 2. Kertoa löydetty ero luvulla n ("pi" \u003d 3,14). Nyt jää vain jakaa tuloksena oleva tuote n-gonin kulmien lukumäärällä. Tarkastellaan näitä laskelmia saman viisikulmion esimerkillä. Joten luku n on 15. Käytämme kaavaa S \u003d n (n - 2): n \u003d 3,14 (15 - 2): 15 \u003d 3,14 ∙ 13: 15 \u003d 2,72. Tämä ei tietenkään ole ainoa tapa laskea kulma radiaaneina. Voit jakaa kulman asteina 57,3: lla. Loppujen lopuksi vain niin monta astetta vastaa yhtä radiaania.

Kulmien laskeminen asteina

Asteiden ja radiaanien lisäksi tavallisen monikulmion kulmien arvoja voidaan yrittää löytää gradienttina. Tämä tehdään seuraavasti. Vähennä 2 kulmien kokonaismäärästä, jaa tulokseksi saatu ero säännöllisen monikulmion sivujen lukumäärällä. Kerro tulos 200: lla. Muuten sellaista kulmien mittayksikköä kuin rakeista ei käytännössä käytetä.

N-gonien ulkoisten kulmien laskeminen

Minkä tahansa normaalin monikulmion osalta, paitsi sisäisen, voit myös laskea ulkoisen kulman. Sen arvo löytyy samalla tavalla kuin muiden lukujen. Joten, jotta löydät normaalin monikulmion ulkokulman, sinun on tiedettävä sisäpuolen merkitys. Lisäksi tiedämme, että näiden kahden kulman summa on aina 180 astetta. Siksi laskelmat tehdään seuraavasti: 180⁰ miinus sisäkulman arvo. Löydä ero. Se on yhtä suuri kuin sen vieressä olevan kulman arvo. Esimerkiksi neliön sisäkulma on 90 astetta, mikä tarkoittaa, että ulkoinen on 180 will - 90⁰ \u003d 90⁰. Kuten näemme, sitä ei ole vaikea löytää. Ulkoisen kulman arvo voi olla välillä + 180⁰ - -180⁰.

Luku, jossa kaikki puolet ovat tasa-arvoisia. Joten esimerkiksi tasasivuinen kolmio on säännöllinen monikulmio, joka koostuu kolmesta suljetusta viivasta. Tässä tapauksessa kaikki sen kulmat ovat 60 °. Sen sivut ovat keskenään tasaiset, mutta eivät yhdensuuntaiset toistensa kanssa. Muilla monikulmioilla on sama ominaisuus, mutta niiden kulmat ovat erikokoisia. Ainoa säännöllinen monikulmio, jonka sivut eivät ole vain tasapuolisia, vaan myös parisuuntaisesti yhdensuuntaisia, on neliö.Jos tehtävässä annetaan tasasivuinen kolmio, jonka pinta-ala on S, sen tuntematon puoli  löytyy kulmien ja sivujen kautta. Ensinnäkin, selvitä kolmion h korkeus, joka on kohtisuorassa sen alustaan \u200b\u200bnähden: h \u003d a * sinα \u003d a√3 / 2, missä α \u003d 60 ° on yksi kulmista kolmiota olevan kannan vieressä. Muunna näiden huomioiden perusteella kaava löytää alue sellaiseksi niin, että sitä voidaan käyttää sivupituuden laskemiseen: S \u003d 1 / 2a * a√3 / 2 \u003d a ^ 2 * √3 / 4 Tästä seuraa, että sivu a on: a \u003d 2√S / √√3

Löydä säännöllisen nelikulman puoli hieman erilaisella menetelmällä. Jos se on neliö, käytä aluetiedona aluetta tai diagonaalia: S \u003d a ^ 2 Siksi puoli a on: a \u003d √ S Lisäksi, jos diagonaali annetaan, niin puoli  voidaan laskea toisella kaavalla: a \u003d d / √2

Useimmissa tapauksissa puoli  oikea monikulmio voidaan määrittää tuntemalla siihen kirjoitetun tai sen ympärillä olevan ympyrän säde. On tiedossa, että kolmion sivun ja ympyrän ympyrän ympyrän säteen välillä on yhteys: a3 \u003d R√3, missä R on piirretyn ympyrän säde. Jos ympyrä on kirjoitettu kolmioon, kaava on erilainen: a3 \u003d 2r√3, missä r on säde piirretty ympyrä Normaalin kuusikulmion tapauksessa kaava, jonka avulla löydetään tunnetun ympyrämäisen (R) tai kirjoitetun (r) ympyrän säde, on seuraava: a6 \u003d R \u003d 2r√3 / 3 Näistä esimerkeistä voidaan päätellä, että mistä tahansa mielivaltaisesta n-gonista kaava löytää osapuolet esillä olevassa muodossa on seuraava: a \u003d 2Rsin (a / 2) \u003d 2rtg (a / 2)

Tärkeimpiä monikulmityyppejä ovat kolmio, suuntauskaavio ja sen tyypit (roma, suorakulmio, neliö), trapetsoidi sekä säännölliset monikulmiot. Jokaisella heistä on oma metodologiansa alueen laskemiseen. Monimutkaisemmat, kuperat ja koverat polygonit jaetaan yksinkertaisiin muotoihin, joiden alueet summataan sitten yhteen.

Monikulmio, jonka pituudet ovat samat kaikilta sivuilta. Siksi, tietäen niiden kokonaispituuden - kehän - (P) ja kärkien tai sivujen kokonaismäärän (n), jaa ensimmäinen toiseen laskeaksesi kunkin koon osapuolet  (a) luvut: a \u003d P / n.

Rinnalla oikein monikulmio  voit kuvata ainoan mahdollisen säteen (R) ympyrän - tätä ominaisuutta voidaan käyttää myös laskettaessa pituus osapuolet  a) mikä tahansa monikulmiojos sen kärkien (n) lukumäärä tunnetaan myös olosuhteista. Tarkastele tätä varten kahden säteen muodostama kolmio ja haluttu puoli. Tämä on tasakulmainen kolmio, josta pohja löytyy kertomalla kahdesti sivun pituus osapuolet  - säde - puoli niiden välisestä kulmasta - keskikulma. Kulman laskeminen on helppoa - jaa 360 ° sivujen lukumäärällä monikulmio. Lopullisen kaavan tulisi näyttää tältä: a \u003d 2 * R * sin (180 ° / n).

Tavallisessa kuperaan monikulmioon kirjoitetulla ympyrällä on samanlainen ominaisuus - se on välttämättä olemassa, ja sädeellä voi olla yksilöllinen arvo jokaiselle tietylle kuvalle. Siksi myös tässä laskettaessa pituutta osapuolet  a) säteen (r) ja sivujen lukumäärän tuntemusta voidaan käyttää monikulmio  (N). Ympyrän ja minkä tahansa sivun kosketuspisteestä piirretty säde on kohtisuorassa tälle puolelle ja jakaa sen puoliksi. Siksi harkitse suorakulmaista kolmiota, jossa säde ja puolet halutusta osapuolet ovat jalat. Määritelmän mukaan niiden suhde on yhtä suuri kuin puolen keskikulman tangentti, jonka voit laskea samalla tavalla kuin edellisessä vaiheessa: (360 ° / n) / 2 \u003d 180 ° / n. Äkillisen kulman tangentin määritelmä suorakulmaisessa kolmiossa voidaan tässä tapauksessa kirjoittaa seuraavasti: tg (180 ° / n) \u003d (a / 2) / r. Ilmaise pituus tästä tasa-arvosta osapuolet. Sinun pitäisi saada tämä kaava: a \u003d 2 * r * tg (180 ° / n).

Monikulmio koostuu useista toisiinsa kytketyistä segmenteistä, jotka muodostavat suljetun linjan. Kaikki tämän luokan luvut on jaettu yksinkertaisiin ja monimutkaisiin. Yksinkertaisiin kuuluu kolmio ja nelikulma, ja monimutkaisiin sisältyy monikulmioita, joissa on suuri määrä osapuoletsamoin kuin tähden monikulmioita.

Käyttöohje

Useimmiten säännöllinen kolmio, jonka kanssa osapuoletvoi. Koska monikulmio on säännöllinen, niin kaikki kolme osapuolets ovat tasa-arvoisia. Siksi, kun tiedät kolmion mediaanin ja korkeuden, löydät kaikki ne osapuolets. Voit tehdä tämän etsimismenetelmällä osapuolets sinin läpi: a \u003d x / cosα osapuoletkolmio s ovat yhtä suuret, ts. a \u003d b \u003d c \u003d a, a \u003d b \u003d c \u003d x / cosα, missä x on korkeus, mediaani tai puolisko. Löydä samoin kaikki kolme tuntematonta osapuolets on tasakulmainen kolmio, mutta yhdellä ehdolla - annettu korkeus. Se tulisi projisoida kolmion pohjalle. Tietäen pohjan korkeus x, löydä osapuolettasakylkisen kolmion a suhteen: a \u003d x / cosα. Koska a \u003d b, koska kolmio on tasakylkinen, etsi se osapuolets seuraavasti: a \u003d b \u003d x / cosα. Kun olet löytänyt sivun osapuoletlaske kolmion kannan pituus Pythagoran lauseen avulla puolella pohjaa: c / 2 \u003d √ (x / cosα) ^ 2- (x ^ 2) \u003d √x ^ 2 (1-cos ^ 2α) / cos ^ 2α \u003d xtgα. Täältä löydät kannan: c \u003d 2xtgα.

Neliö on säännöllinen nelikulma, osapuoletne lasketaan useilla tavoilla. Jokainen niistä kuvataan alla: Ensimmäinen menetelmä ehdottaa löytämistä osapuolets neliön diagonaalin poikki. Koska kaikki neliön kulmat ovat suorat, tämä diagonaali jakaa ne kahteen osaan siten, että muodostuu kaksi suorakulmaista kolmiota, joiden kulma alustassa on 45 astetta. Niinpä osapuoletja neliö on: a \u003d b \u003d c \u003d f \u003d d * cosα \u003d d√2 / 2, missä d on neliön diagonaali. Jos neliö on merkitty ympyrään, tietäen tämän ympyrän säteen, löydä se osapuolety: a4 \u003d R√2, missä R on ympyrän säde.

On paljon osapuoletne monikulmioita osapuolety laske viimeinen ehdotetuista menetelmistä - syöttämällä monikulmio  ympyrässä. Voit tehdä tämän piirtämällä normaalin monikulmion mielivaltaisella tavalla osapuolets, ja sen ympärillä kuvaillaan ympyrä, jolla on tietty säde R. Kuvittele, että tehtävässä on annettu joitain mielivaltaisia \u200b\u200bn-gon-muotoja. Jos ympyrä on rajoitettu siitä monikulmiositten löytää osapuoletkäytät kaavaa: an \u003d 2Rsinα / 2.