Дослідницька робота "Обчислення площі багатокутника на картатому папері"

Обчислення площ фігур на аркуші у клітку. Формула Піка.

А чи є завдання, які не схожі на завдання зі шкільних підручників? Так, це завдання на папері. У завданнях, які будуть на ЄДІ є ціла група завдань, в яких дано багатокутник, побудований на аркуші в клітинку і стоїть питання про знаходження площі. Масштаб клітки це один квадратний сантиметр. Для знаходження площ таких фігур можна використати формулу Піка. За допомогою цієї формули такі завдання вирішуються за хвилину, що дозволяє на іспитах приділити більше часу складнішим завданням.

Формула піка

Площу шуканої фігури можна знайти за формулою:

М – кількість вузлів на межі трикутника (на сторонах та вершинах)

N – кількість вузлів усередині трикутника

*Під «вузлами» мається на увазі перетин ліній.

Знайдемо площу трикутника:

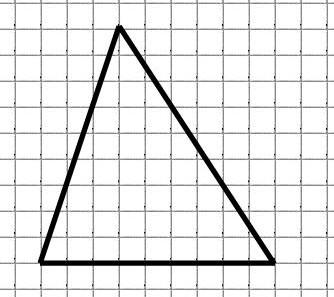
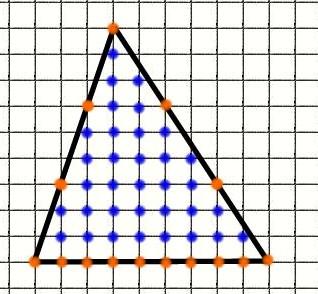
Зазначимо вузли:

1 клітина = 1 см M = 15 (позначено червоним) N = 34 (позначено синім)

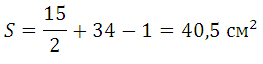
Завдання:

Знайдемо площу багатокутника:

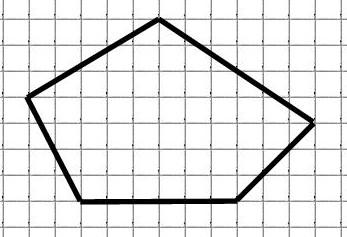
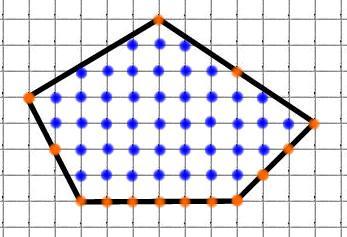
Зазначимо вузли:

M = 14 (позначено червоним) N = 43 (позначено синім)

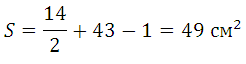
Бібліографічний опис:Татьяненко А. А., Тетьяненко С. А. Обчислення площ постатей, зображених на картатому папері // Юний вчений. - 2016. - №3..09.2017).

Під час підготовки до основного державного іспиту я зустрівся із завданнями, в яких потрібно обчислити площу фігури, зображеної на картатому аркуші паперу. Як правило, ці завдання не викликають великих труднощів, якщо фігура є трапецією, паралелограмом або трикутником. Досить добре знати формули обчислення площ цих фігур, порахувати кількість клітинок і обчислити площу. Якщо фігура є деяким довільним багатокутником, то тут необхідно використовувати особливі прийоми. Мене зацікавила ця тема. І природно виникли питання: де у повсякденному житті можуть виникнути завдання на обчислення площ на папері? У чому особливість таких завдань? Чи існують інші методи чи універсальна формула для обчислення площ геометричних фігур, зображених на папері?

Вивчення спеціальної літератури та інтернет джерел показало, що існує універсальна формула, що дозволяє обчислити площу фігури, зображеної на клітці. Ця формула називається формулою Піка. Однак, у рамках шкільної програми дана формула не розглядається, незважаючи на свою простоту у застосуванні та отриманні результату. Більше того, мною проведено опитування друзів та однокласників (у двох формах: при особистій розмові та в соціальних мережах), у якому взяли участь 43 учнів шкіл міста Тобольська. Дане опитування показало, що лише одна людина (учень 11 класу) знайома з формулою Піка для обчислення площ.

Нехай задана прямокутна система координат. У цій системі розглянемо багатокутник, який має цілі координати. У навчальній літературі точки з цілими координатами називаються вузлами. Причому багатокутник не обов'язково має бути опуклим. І нехай потрібно визначити його площу.

Можливі такі випадки.

1. Фігура є трикутником, паралелограм, трапецією:

1) підраховуючи клітини необхідно визначити висоту, діагоналі або сторони, які потрібні для обчислення площі;

2) підставити знайдені величини формулу площі.

Наприклад, потрібно обчислити площу фігури, зображеної малюнку 1 з розміром клітини 1см на 1 див.

Мал. 1. Трикутник

Рішення. Підраховуємо клітини і знаходимо: . За формулою отримуємо: .

2 Фігура є багатокутником

Якщо фігура є багатокутником, то можна використовувати такі методи.

Метод розбиття:

1) розбити багатокутник на трикутники, прямокутники;

2) обчислити площі одержаних фігур;

3) визначити суму всіх площ отриманих фігур.

Наприклад, потрібно обчислити площу фігури, зображеної малюнку 2 з розміром клітини 1см на 1 см методом розбиття.

Мал. 2. Багатокутник

Рішення. Способів розбиття існує безліч. Ми розіб'ємо фігуру на прямокутні трикутники і прямокутник, як показано на малюнку 3.

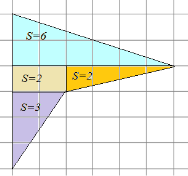
Мал. 3. Багатокутник. Метод розбиття

Площі трикутників рівні: , , , площа прямокутника - . Складаючи площі всіх фігур отримаємо:

Метод додаткової побудови

1) добудувати фігуру до прямокутника

2) знайти площі отриманих додаткових фігур та площу самого прямокутника

3) від площі прямокутника відняти площі всіх «зайвих» фігур.

Наприклад, потрібно обчислити площу фігури, зображеної малюнку 2 з розміром клітини 1см на 1 см методом додаткової побудови.

Рішення. Добудуємо нашу фігуру до прямокутника, як показано на малюнку 4.

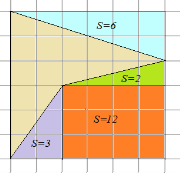
Мал. 4. Багатокутник. Метод доповнення

Площа великого прямокутника дорівнює прямокутника, розташованого всередині - , площі «зайвих» трикутників , , Тоді площа шуканої фігури.

При обчисленні площ багатокутників на картатому папері можливо використовувати ще один метод, який носить назву формула Піка на прізвище вченого, який її відкрив.

Формула Піка

Нехай у багатокутника, зображеного на картатому папері, лише цілочисленні вершини. Точки у яких обидві координати цілі називаються вузлами ґрат. Причому багатокутник може бути як опуклим, так і непуклим.

Площа багатокутника з цілими вершинами дорівнює , де B - кількість цілих точок всередині багатокутника, а Г - кількість цілих точок на межі багатокутника.

Наприклад, для багатокутника, зображеного малюнку 5.

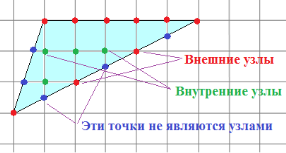
Мал. 5. Вузли у формулі Піка

Наприклад, потрібно обчислити площу фігури, що зображена на малюнку 2 з розміром клітини 1см на 1 см за формулою Піка.

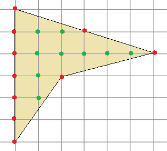
Мал. 6. Багатокутник. Формула Піка

Рішення. На малюнку 6: В=9, Г=10, тоді за формулою Піка маємо:

Нижче наведено приклади деяких завдань, розроблених автором на обчислення площ фігур, зображених на папері.

1. У дитячому садкудіти зробили аплікації батькам подарунок (рис.7). Знайдіть площу аплікації. Розмір кожної клітини дорівнює 1см  1см.

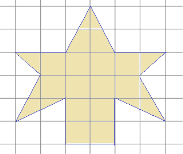
Мал. 7. Умова задачі 1

2. Один гектар ялинових насаджень може затримувати на рік до 32 т пилу, соснових – до 35 т, в'яза – до 43 т, дуба – до 50 т. Бука – до 68 т. Порахуйте, скільки тонн пилу затримає ялинник за 5 років. План ялинника зображено малюнку 8 (масштаб 1 див. - 200 м.).

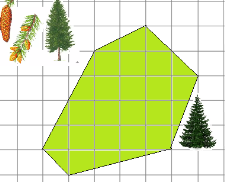
Мал. 8. Умова задачі 2

3. В орнаментах хантів та мансі, переважають геометричні мотиви. Часто зустрічаються стилізовані зображення тварин. На малюнку 9 зображено фрагмент мансійського орнаменту "Заячі вушка". Обчисліть площу зафарбованої частини орнаменту.

Мал. 9. Умова задачі 3

4. Потрібно пофарбувати стіну заводської будівлі (рис. 10). Розрахуйте потрібну кількість водоемульсійної фарби (у літрах). Витрата фарби: 1 літр на 7 кв. метрів Масштаб 1см – 5м.

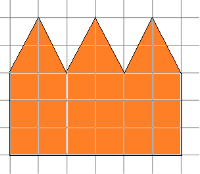
Мал. 10. Умова задачі 4

5. Зірчастий багатокутник – плоска геометрична фігура, Складена з трикутних променів, що виходять із загального центру, що зливаються в точці сходження. На особливу увагу заслуговує п'ятикутна зірка - пентаграма. Пентаграма – це символ досконалості, розуму, мудрості та краси. Це найпростіша форма зірки, яку можна зобразити одним розчерком пера, жодного разу не відірвавши його від паперу і при цьому жодного разу не пройшовши двічі по одній лінії. Намалюйте п'ятикутну зірочку не відриваючи олівця від аркуша картатого паперу, так, щоб усі кути багатокутника, що вийшов, знаходилися у вузлах клітини. Обчисліть площу отриманої фігури.

Проаналізувавши математичну літературу і розібравши велику кількість прикладів на тему дослідження, я дійшов висновку, що вибір методу обчислення площі фігури на папері залежить від форми фігури. Якщо фігура є трикутником, прямокутником, паралелограмом або трапецією, то зручно скористатися всіма відомими формулами для обчислення площ. Якщо фігура є опуклий багатокутник, то можна використовувати як метод розбиття, так і доповнення (у більшості випадків зручніше - метод доповнення). Якщо фігура є неопуклим або зірчастим багатокутником, то зручніше застосувати формулу Піка.

Оскільки формула Піка є універсальною формулою для обчислення площ (якщо вершини багатокутника знаходяться у вузлах ґрат), то її можна використовувати для будь-якої фігури. Однак, якщо багатокутник займає досить велику площу (або дрібні клітини), то велика ймовірність припуститися помилки в підрахунках вузлів решітки. Взагалі, в ході дослідження, я дійшов висновку, що при вирішенні подібних завдань в ОДЕ краще скористатися традиційними методами(Розбиття або доповнення), а результат перевірити за формулою Піка.

Література:

Вавілов В. В., Устинов А. В. Багатокутники на ґратах. – М.: МЦНМО, 2006. – 72 с.
Васильєв І. Н. Навколо формули Піка// Науково-популярний фізико-математичний журнал «Квант». - 1974. - №12. Режим доступу: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
Жарковська Н., Рісс Е. Геометрія картатого паперу. Формула Піка. // Перше вересня. Математика. – 2009. – № 23. – с.24,25.

У рамках цієї статті розглянуто одне із занять елективного курсу з математики «Наочна геометрія» для учнів 6 класу. Заняття супроводжується показом презентації (Додаток).

Ця тема буде також цікава учням 10-11 класів у рамках підготовки до ЄДІ. Формулу Піка можна застосовувати при обчисленні площі фігури, зображеної на папері в картаті (це завдання В3 в контрольно-вимірювальних матеріалах ЄДІ).

Хід уроку

Вчитель:Роздуми над якимось завданням часто призводять до захоплення математикою. А чи є завдання, які не схожі на завдання зі шкільних підручників? Так, це завдання на папері. Такі завдання є у контрольно-вимірювальних матеріалах ЄДІ. У чому полягає особливість таких завдань, які методи і прийоми використовуються на вирішення завдань на картатий папері? На цьому занятті ми досліджуємо завдання на папері, пов'язані зі знаходженням площі зображеної фігури, і навчимося обчислювати площі багатокутників, намальованих на картатому листку.

Вчитель:Об'єктом дослідження будуть завдання на папері.

Предметом нашого дослідження будуть завдання на обчислення площі багатокутників на папері.

І метою дослідження буде формула Піка. Це зручна формула, за допомогою якої можна обчислити площу будь-якого багатокутника без самоперетинів з вершинами у вузлах картатого паперу.

Вчитель:Сформулюємо гіпотезу: площа фігури, обчислена за формулою Піка, дорівнює площі фігури, обчисленої за формулами геометрії.

При розв'язанні завдань на папері для паперу нам знадобиться геометрична уява і досить прості відомості, які нам відомі:

Площа прямокутника дорівнює добутку суміжних сторін.
Площа прямокутного трикутника дорівнює половині добутку сторін, що утворюють прямий кут.

Вчитель:Хто ж такий Пік? Пік Георг Олександров (1859–1943 рр.) – австрійський математик. Відкрив формулу 1899 року.

Формула Піка: S = B + – 1, де S – площа багатокутника, з вершинами у вузлах квадратної сітки; Г – кількість вузлів сітки, що лежать на межах багатокутника (на сторонах та у вершинах), В – кількість вузлів сітки, що лежать усередині багатокутника.

Вчитель:Вузли сітки – точки, де перетинаються лінії сітки.

Внутрішні вузли багатокутника – червоні. Вузли на межах багатокутника – зелені.

Розглянемо тільки такі багатокутники, всі вершини яких лежать у вузлах картатого паперу (Додаток).

Вчитель:Проведемо дослідження для трикутника. Спочатку порахуємо площу трикутника за формулою Піка (Додаток).

Вчитель:Тепер порахуємо площу трикутника за формулами геометрії. Площа будь-якого трикутника, намальованого на папері, легко порахувати, представивши її як суму або різницю площ прямокутних трикутників і прямокутників, сторони яких йдуть по лініях сітки, що проходять через вершини намальованого трикутника. Учні виконують обчислення у зошитах. Потім перевіряють свої результати з обчисленнями на слайді (Додаток).

Вчитель:Давайте повторимо дослідження для 4-кутника (Додаток).

Вчитель:А тепер повторимо дослідження для 5-кутника (Додаток).

Вчитель:А тепер розглянемо багатокутник у формі ракети. Отримуємо, що формула Піка буде справедлива і довільного багатокутника (Додаток).

Вчитель:Порівнявши результати досліджень, зробіть висновок. Отримали, що площа фігури, обчислена за формулою Піка, дорівнює площі фігури, що обчислена за формулами геометрії. Отже, гіпотеза виявилася вірною.

Далі вчитель пропонує обчислити площу «свого» довільного багатокутника за формулами геометрії та за формулою Піка та порівняти отримані результати. "Пограти" з формулою Піка можна на сайті математичних етюдів (http://www.etudes.ru).

На закінчення статті пропонується одна з робіт на тему «Обчислення площі довільного багатокутника за допомогою формули Піка» (Додаток).

Муніципальне бюджетне освітня установа

«Урдомська ЗОШ»

Тема дослідження:

«Обчислення площі багатокутника на папері»

7 клас

Науковий керівник: Тончихіна Ганна Степанівна,

учитель математики.

2013-2014 навчальний рік

Зміст

Вступ………………………………………………………

Результати дослідження ……………………………………

Заключение……………………………………………………

Література……………………………………………………

Вступ

"Предмет математики настільки серйозний,

що корисно не втрачати нагоди

робити його трохи цікавим"

Б. ПАСКАЛЬ

Вперше з проблемою обчислення площі фігур я зіткнувся при вирішенні задачі, суть якої зводилася до того, що потрібно було розділити квадрат на п'ять частин так, щоб площа п'яти фігур мала загальну вершину, однакову площу та рівну довжину по периметру. Рішення вимагало наочний креслення. Оскільки рішення виконувалося у зошиті, то мене зацікавило: чи можна розрахувати площу, порахувавши клітини всередині фігури. Як, виявилося, існує формула, яка дозволяє порахувати площу, але тільки не за клітинами, а за їхніми вузлами – формула Піка. Згодом мені захотілося дізнатися, чи є інші способи обчислення площі на папері.

Я висунув гіпотезу: якщо геометрична фігура зображена на папері, то її площу можна обчислити у різний спосібта переконатися, що результати обчислень будуть однаковими.

Мета роботи: Вивчення способів обчислення площ фігур на картатому папері.

Для досягнення поставленої мети необхідне вирішення наступних завдань:

Вивчити літературу з досліджуваної теми.

Відібрати цікаву та зрозумілу інформацію для дослідження.

Знайти різні методита прийоми обчислення площі багатокутників на папері.

Проаналізувати та систематизувати отриману інформацію.

Створити електронну презентацію роботи для представлення зібраного матеріалу.

Об'єкт дослідження: завдання на обчислення площі багатокутника на папері.

Предмет дослідження: способи обчислення площі багатокутника на папері.

Методи та дослідження: моделювання, порівняння, узагальнення, аналогії, аналіз та класифікація інформації.

Традиційно вважається, що родоначальниками геометрії як систематичної науки є стародавні греки, які перейняли у єгиптян ремесло землеміру та вимірювання обсягів тіл і перетворили його на сувору наукову дисципліну. Вимірювання площ вважають одним із найдавніших розділів геометрії, зокрема назву «геометрія» (тобто «землемірство») пов'язують саме з виміром площ. Багато вчених вирішували проблему обчислення площі фігури. В історію з поняттям площі увійшли імена Евкліда, Архімеда, Піфагора, Герона Олександрійського, Рене Декарта, П'єра Ферма, Георга Піка та ін. Ними відкрито велику кількість різних формул і способів обчислення площі фігури.

Поняття площі нам відоме з повсякденного досвіду. Наприклад, кожен розуміє сенс слів: площа кімнати дорівнює двадцяти квадратних метрів. Мене цікавить площа багатокутника – величина тієї частини площини, що займає багатокутник. Вимірювання площ проводиться за допомогою вибраної одиниці виміру. За одиницю виміру площ приймають квадрат, сторона якого дорівнює одиниці виміру відрізків. При вибраній одиниці виміру площ площа кожного багатокутника виражається позитивним числом. Якщо багатокутник складено з кількох багатокутників, його площа дорівнює сумі площ цих багатокутників. Про цю властивість площі говорив ще Евклід.

Загальний метод для знаходження площі довільного багатокутника полягає в тому, що його треба розбити на трикутники, обчислити їхні площі та скласти результати. Іноді багатокутник представляють як суму та різницю трикутників. Однак простий та компактний формули для визначення площі довільного n-кутника немає. Багатокутник на папері є одним з видів довільного n-кутника.

Я приступив до вивчення обчислення площ багатокутників на папері, і виявилося, завдання досить різноманітні і цікаві. Вони змушують думати, розмірковувати, аналізувати, шукати аналогії.

Результати дослідження

У процесі дослідження я навчився знаходити площі багатокутників на папері 4 різними способами:

перший спосіб – розбиття багатокутника на прямокутні трикутники та (або) прямокутники з вершинами у вузлах сітки;

другий спосіб - полягає в тому, що від площі основного прямокутника віднімаються площі прямокутних трикутників та (або) прямокутників;

третій спосіб - обчислення площі багатокутника з вершинами у вузлах картатого паперу за формулою Піка;

четвертий метод – підрахунок площі фігури, ввівши систему координат.

П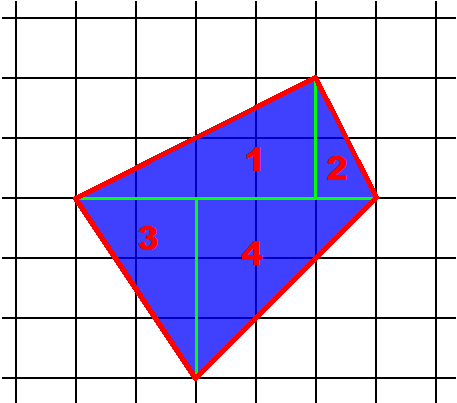

ервий спосіб - розбиття

Сенс цього способу полягає в тому, що багатокутник розрізається на прямокутники та (або) прямокутні трикутники з вершинами у вузлах сітки.

Розділимо чотирикутник на чотири прямокутні трикутники (рис.1).

Рис.1

Айдемо площу першого трикутника – S 1 =½*4*2=4

Айдемо площу другого трикутника – S 2 =½*1*2=1

Знайдемо площу третього трикутника – S 3 =½*3*2=3

Знайдемо площу четвертого трикутника – S 4 =½*3*3=4,5

Знайдемо площу чотирикутника – S =S 1 +S 2 +S 3 +S 4 =4+1+3+4,5=12,5

Відповідь: 12,5

У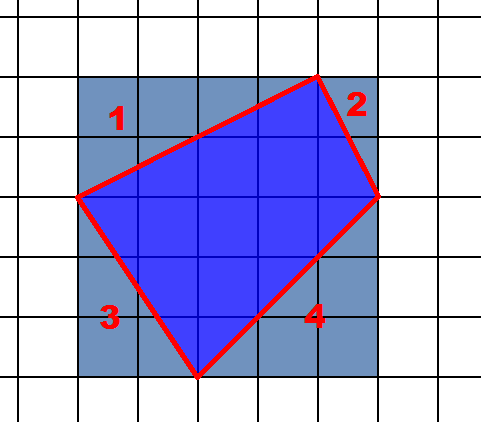

торий спосіб - доповнення до прямокутника

Сенс цього способу - це доповнення багатокутника до прямокутника, а потім віднімання зайвих частин.

Рис.2

Добудуємо прямокутника так, щоб його сторони проходили через вершини чотирикутника. Отримали квадрат із стороною 5 (рис.2).

2.Знайдемо площу квадрата S кв = 5 2 = 25

3.Знайдемо площу першого трикутника – S 1 =½*4*2=4

4.Знайдемо площу другого трикутника – S 2 =½*1*2=1

5.Знайдемо площу третього трикутника – S 3 =½*3*2=3

6.Знайдемо площу четвертого трикутника – S 4 =½*3*3=4,5

7. Знайдемо площу чотирикутника –

S = S кв - (S 1 + S 2 + S 3 + S 4) = 25 - (4 +1 +3 +4,5) = 12,5

Відповідь: 12,5

Т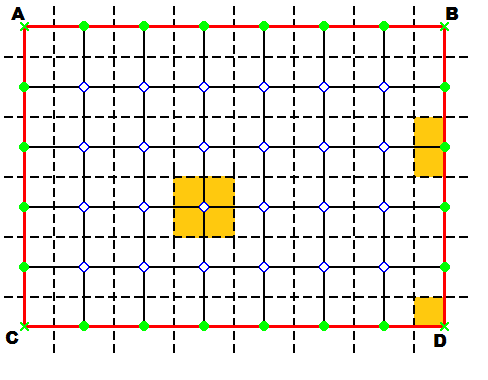

третій спосіб - формула Піка

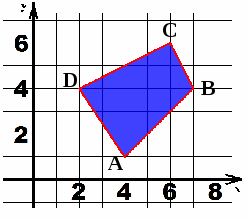
Нехай ABCD - прямокутник з вершинами у вузлах і сторонами, що йдуть лініями сітки (рис.3).

Про

Рис.3

Позначимо через aкількість вузлів, що лежать усередині прямокутника, а через b – кількість вузлів з його межі. Змістимо сітку на півклітини вправо і півклітини вниз. Тоді територію прямокутника можна «розподілити» між вузлами так: кожен з авузлів «контролює» цілу клітинку зміщеної сітки, а кожен з bвузлів – 4 граничні не кутові вузли – половину клітини, а кожна з кутових точок – чверть клітини. Тому площа прямокутника S дорівнює

S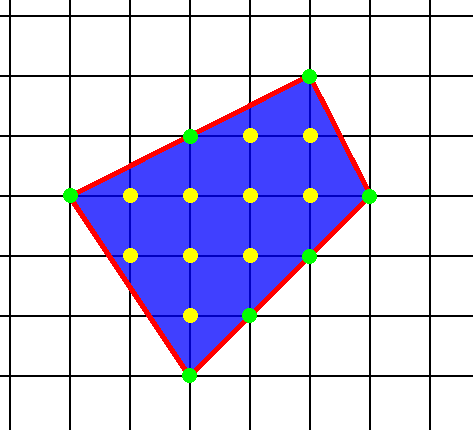

= a + (b - 4): 2 + 4 · 1/4 = a + b /2 - 1.

Виявляється, ця формула вірна не тільки для прямокутників, а й для довільних багатокутників з вершинами у вузлах сітки!

Рис.4

Це співвідношення відкрив і довів австрійський математик Георг Олександр Пік (Georg Alexander Pick) у 1899 році.

Рас з читаємо площу нашого чотирикутника за формулою Піка (рис.4):

кількість вузлів, що лежать усередині - а = 10,

кількість вузлів на кордоні - b = 7,

S = 10 +7/2-1 = 12,5

Відповідь: 12,5

Четвертий спосіб - знаходження площі за координатами вершин

У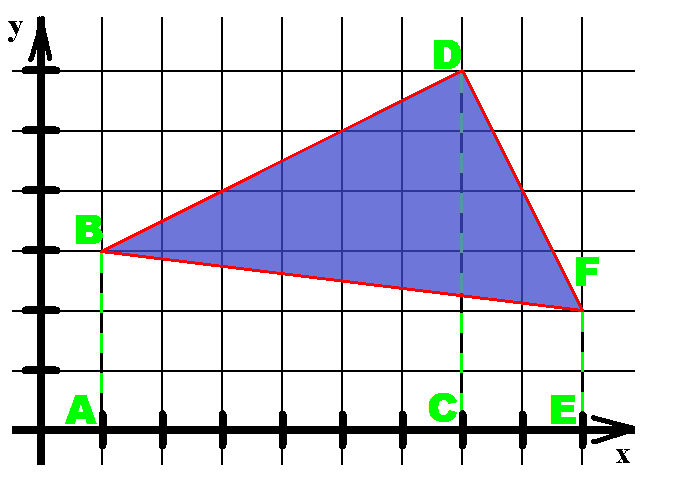

основі даного способу лежить метод координат, запропонований у XVII столітті французькими математиками Рене Декартом (1596-1650) та П'єром Ферма (1601-1665), що дозволяє перекладати геометричні поняття алгебраїчною мовою. В основі цього лежить поняття – система координат. Ми розглядатимемо обчислення площі трикутника за координатами його вершин у прямокутній системі координат:

B ( x 1 ; y 1 );

F ( x 2 ; y 2 );

D ( x 3 ; y 3 )

S фігури = S ABDC +S CDEF -S ABEF =

(

Рис.5

AB+CD)/2*AC+ (CD+EF)/2*CE-

- (AB+EF)/2*AE =

= (y 1 +y 3 )/2*(x 3 -x 1 ) + (y 3 +y 2 )/2*(x 2 -x 3 )-(y 1 +y 2 )/2*(x 2 -x 1 ) =

=½(y 1 x 3 -y 1 x 1 +y 3 x 3 -y 3 x 1 +y 3 x 2 - -y 3 x 3 +y 2 x 2 -y 2 x 3 -y 1 x 2 +y 1 x 1 -y 2 x 2 +y 2 x 1 ) =

Рис.6

½(y 1 x 3 -y 3 x 1 +y 3 x 2 -y 2 x 3 -y 1 x 2 +y 2 x 1 )= =½((x ₁ y ₂ +x ₂ y ₃ +x ₃ y ₁ )-(x ₂ y ₁ +x ₃ y ₂ +x ₁ y ₃ ))

Хоча формула і виведена для трикутника, неважко показати, що вона придатна для обчислення площі будь-якого n-кутника. Щоб розрахувати площу багатокутника даним способом необхідно діяти за таким алгоритмом:

1.Використовуючи наш чотирикутникABCD(рис.6), як приклад, запишемо координати по осях X і Y кожної вершини багатокутника у напрямку читання проти годинникової стрілки, продублювавши координати першої вершини внизу списку

Таблиця 1

Таблиця 2

2. Помножимо значення координати “X” кожної вершини на значення “Y” наступної вершини (таблиця №1).Складемоотримані твори: 4*4+7*6+6*4+2*1= 84

3. Помножимо значення координати "Y" кожної вершини на значення "X" наступної вершини (таблиця №2). Складемо отримані твори:

1*7 + 4*6 + 6*2 + 4*4 = 59

4. Віднімаємо суму, отриману у кроці 3 з результату, отриманого у кроці 2:(84) - (59) = 25

5. Розділимо цю різницю на 2, щоб отримати площу чотирикутника: S = 25/2 = 12,5 .

Відповідь: 12,5

Всі розглянуті способи знаходження площі цієї постаті привели нас до того самого результату.

Обчислення площі неопуклого багатокутника

П 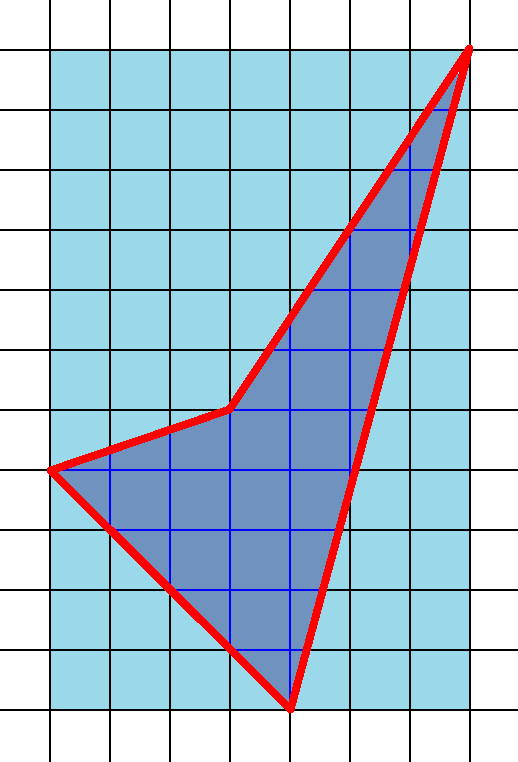ервий спосібне підходить даної постаті, т.к. неможливо розбити на прямокутники та (або) прямокутні трикутники з вершинами у вузлах сітки.

Другий спосіб

зі сторонами 7 та 11. (рис.7)

3.Знайдемо площу першого трикутника – S 1 =½*4*4=8

Рис.7

.Знайдемо площу другого трикутника – S 2 =½*3*11=16,5

5.Знайдемо площу третього трикутника – S 3 =½*3*1=1,5

6.Знайдемо площу прямокутника – S 4 =3*6=18

7.Знайдемо площу першого трикутника – S 5 =½*4*6=12

8.Знайдемо площу шуканого чотирикутника -

S = S пр - (S1 + S2 + S3 + S4 + S5) = 77-

-(8+16,5+1,5+18+12)=21

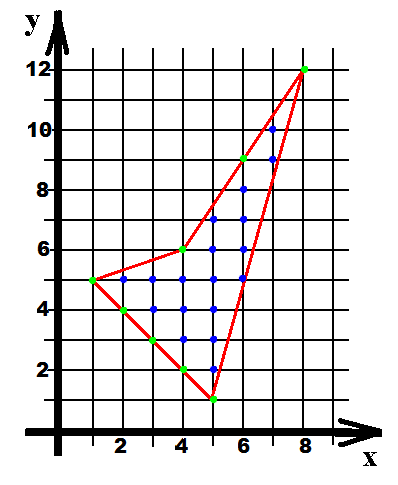
Про

Рис.8

Твіт: 21

Третій спосіб

кількість вузлів, що лежать усередині - а = 18, кількість вузлів на кордоні - b = 8 (рис.8),

S=a+b/2-1, S=18+8/2-1=21

Відповідь: 21

Четвертий спосіб

S=½(( x₁y₂+ x₂y₃+ x₃y 4 + x 4 y 1 )-(x₂y₁+ x₃y₂+ x 4 y₃+ x 1 y 4 ))

S =½((1*1+5*12+8*6+4*5)-(5*5+8*1+4*12+1*6)) =21

І знову ми отримали один і той самий результат.

Порівняльний аналіз способів знаходження площі багатокутника на папері.

Розбиття

Доповнення до прямокутника

Формула Піка

За координатами вершин

Плюси

(+)

Простота підрахунку площі фігур, які розбиваються на прямокутники та (або) прямокутні трикутники з вершинами у вузлах сітки.

Простота підрахунку площі при невеликій кількості фігур, площу яких необхідно відібрати

Обчислення площі багатокутників із незвичайною формою.

Невелика кількість вершин і фігура не розбивається на прямокутники та прямокутні трикутники з вершинами у вузлах сітки.

Короткість формули:

S = a + b / 2-1

Невелика кількість вершин і фігура з великою кількістю вузлів та наявність спірних вузлів.

Простота алгоритму

Мінуси

(-)

Безліч дій.

Складність підрахунку площі багатокутників незвичайної форми.

Велика кількість фігур, площу яких необхідно відібрати

Фігури із великою кількістю вузлів.

Підрахунок площі фігур із великою кількістю вершин.

Неможливість підрахунку площі фігур, які не розбиваються на прямокутники та (або) прямокутні трикутники з вершинами у вузлах сітки.

«Спірні» вузли:

Вузли, що лежать близько до багатокутника.

Висновок

У ході цієї роботи я розширив свої знання щодо вирішення завдань на картатий папері та знаходження площ фігур і переконався у різноманітті способів обчислення площі багатокутника.

Крім розглянутих мною у цій роботі 4 способів є й інші.

Досліджуване мною питання досить цікаве, корисне, але дуже об'ємне.

Завдання на картатому папері зустрічаються в завданнях ЄДІ та ОДЕ, тому слід добре знати жоден спосіб обчислення площі багатокутника.

Цілі та завдання, поставлені на початку роботи, були виконані. Хочу зазначити, що будь-який із розглянутих мною способів застосуємо для вирішення завдань.

Вважаю, з цією роботою слід познайомити однокласників, оскільки це допоможе їм під час підготовки до іспитів.

Література:

Атанасян Л. С. Геометрія 7-9, підручник. - М.Просвіта,2009

Площа багатокутників.