تعرف على طول القطر من خلال معرفة أضلاع المضلع المنتظم. مضلع منتظم. عدد أضلاع المضلع المنتظم

مثلث ، مربع ، مسدس - هذه الأشكال معروفة للجميع تقريبًا. لكن لا يعرف الجميع ما هو المضلع العادي. ولكن هذا هو نفس المضلع العادي يسمى المضلع الذي له زوايا وجوانب متساوية. هناك الكثير من هذه الأشكال ، لكن جميعها لها نفس الخصائص ، وتنطبق عليها نفس الصيغ.

خصائص المضلع المنتظم

يمكن كتابة أي مضلع منتظم ، سواء كان مربعًا أو مثمنًا ، في دائرة. غالبًا ما تُستخدم هذه الخاصية الأساسية عند إنشاء شكل. بالإضافة إلى ذلك ، يمكن كتابة دائرة في شكل مضلع. في هذه الحالة ، سيكون عدد نقاط الاتصال مساويًا لعدد جوانبها. من المهم أن يكون للدائرة المنقوشة في مضلع منتظم مركز مشترك معها. هؤلاء الأشكال الهندسية تخضع لنظرية واحدة. يرتبط أي جانب من أضلاع n-gon العادي بنصف قطر الدائرة المحصورة R. لذلك ، يمكن حسابه باستخدام الصيغة التالية: a \u003d 2R ∙ sin180 °. من خلال يمكنك العثور ليس فقط على الجوانب ، ولكن أيضًا على محيط المضلع.

كيفية إيجاد عدد أضلاع مضلع منتظم

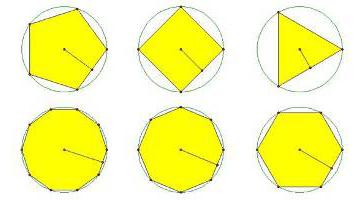أي واحد يتكون من عدد معين من الأجزاء المتساوية ، والتي ، عند الاتصال ، تشكل خطًا مغلقًا. في هذه الحالة ، جميع زوايا الشكل المُشكَّل لها نفس القيمة. تنقسم المضلعات إلى بسيطة ومعقدة. تتضمن المجموعة الأولى مثلثًا ومربعًا. المضلعات المعقدة لها جوانب أكثر. وتشمل أيضًا شخصيات على شكل نجمة. بالنسبة للمضلعات المنتظمة المعقدة ، يتم العثور على الجوانب من خلال كتابتها في دائرة. هنا دليل. ارسم مضلعًا منتظمًا بعدد عشوائي من الأضلاع n. ارسم دائرة حوله. أعط نصف القطر R. الآن تخيل أنك حصلت على بعض n-gon. إذا كانت نقاط أركانها تقع على دائرة ومتساوية مع بعضها البعض ، فيمكن إيجاد الجانبين بالصيغة: a \u003d 2R ∙ sinα: 2.

إيجاد عدد أضلاع مثلث منتظم منقوش

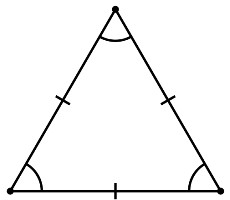
المثلث متساوي الأضلاع هو مضلع منتظم. تنطبق الصيغ عليها كما في المربع و n-gon. يعتبر المثلث صحيحًا إذا كان له نفس الطول. في هذه الحالة ، الزوايا تساوي 60. لنقم ببناء مثلث بطول ضلع معطى a. بمعرفة متوسطها وارتفاعها يمكنك معرفة معنى أضلاعها. للقيام بذلك ، سنستخدم طريقة إيجاد الصيغة a \u003d x: cosα ، حيث x هو الوسيط أو الارتفاع. بما أن كل جوانب المثلث متساوية ، نحصل على أ \u003d ب \u003d ج. عندئذٍ ستكون العبارة التالية صحيحة a \u003d b \u003d c \u003d x: cosα. وبالمثل ، يمكنك إيجاد قيمة الأضلاع في مثلث متساوي الساقين ، لكن x سيكون الارتفاع المعطى. في هذه الحالة ، يجب إسقاطها بدقة على قاعدة الشكل. إذن ، بمعرفة الارتفاع x ، نجد الضلع a في المثلث متساوي الساقين بالصيغة a \u003d b \u003d x: cosα. بعد إيجاد قيمة a ، يمكنك حساب طول القاعدة c. دعنا نطبق نظرية فيثاغورس. سنبحث عن قيمة نصف القاعدة c: 2 \u003d √ (x: cosα) ^ 2 - (x ^ 2) \u003d √x ^ 2 (1 - cos ^ 2α): cos ^ 2α \u003d x tgα. ثم ج \u003d 2xtgα. بهذه الطريقة البسيطة ، يمكنك إيجاد عدد أضلاع أي مضلع منقوش.

حساب جوانب مربع منقوش في دائرة

مثل أي مضلع منتظم منقوش آخر ، المربع له جوانب وزوايا متساوية. تنطبق نفس الصيغ عليه بالنسبة للمثلث. يمكنك حساب جوانب المربع باستخدام قيمة القطر. دعنا نفكر في هذه الطريقة بمزيد من التفصيل. من المعروف أن القطر يقسم الزاوية إلى نصفين. في البداية ، كانت قيمتها 90 درجة. وهكذا ، بعد القسمة ، يتكون اثنان وتكون زاياهما عند القاعدة 45 درجة. وفقًا لذلك ، سيكون كل جانب من جوانب المربع متساويًا ، أي: a \u003d b \u003d c \u003d q \u003d e ∙ cosα \u003d e√2: 2 ، حيث e هو قطري المربع ، أو قاعدة المثلث القائم الزاوية المكونة بعد القسمة. هذه ليست الطريقة الوحيدة لإيجاد جوانب المربع. دعونا نكتب هذا الشكل في دائرة. بمعرفة نصف قطر هذه الدائرة R ، نجد ضلع المربع. سنحسبها على النحو التالي a4 \u003d R√2. يتم حساب نصف قطر المضلعات المنتظمة بالصيغة R \u003d a: 2tg (360 o: 2n) ، حيث a هو طول الضلع.

كيفية حساب محيط n-gon

محيط n-gon هو مجموع أضلاعه. ليس من الصعب حسابها. للقيام بذلك ، تحتاج إلى معرفة معاني جميع الأطراف. توجد صيغ خاصة لبعض أنواع المضلعات. إنها تسمح لك بإيجاد المحيط بشكل أسرع. من المعروف أن أي مضلع منتظم له جوانب متساوية. لذلك ، لحساب محيطه ، يكفي معرفة واحد منهم على الأقل. تعتمد الصيغة على عدد جوانب الشكل. بشكل عام ، يبدو الأمر كما يلي: P \u003d an ، حيث a هي قيمة الضلع ، و n هي عدد الزوايا. على سبيل المثال ، للعثور على المحيط مثمن منتظم مع ضلع 3 سم ، من الضروري ضربه في 8 ، أي P \u003d 3 ∙ 8 \u003d 24 سم. بالنسبة لمسدس ضلع يبلغ طوله 5 سم ، نحسب كالتالي: P \u003d 5 6 \u003d 30 سم ، وهكذا لكل مضلع.

إيجاد محيط متوازي أضلاع ومربع ومعين

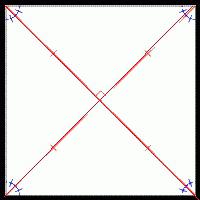
اعتمادًا على عدد جوانب المضلع المنتظم ، يتم حساب محيطه. هذا يجعل المهمة أسهل بكثير. في الواقع ، على عكس الشخصيات الأخرى ، في هذه الحالة لا تحتاج إلى البحث عن جميع جوانبها ، يكفي واحد. بنفس المبدأ ، نجد محيط المربعات ، أي المربع والمعين. على الرغم من أن هذا شخصيات مختلفة، الصيغة الخاصة بهم هي P \u003d 4a ، حيث a هو أحد الضلع. دعنا نعطي مثالا. إذا كان طول ضلع معين أو مربع يساوي 6 سم ، فسنوجد المحيط كما يلي: P \u003d 4 ∙ 6 \u003d 24 سم ، متوازي الأضلاع له أضلاع متقابلة متساوية. لذلك ، تم إيجاد محيطه بطريقة مختلفة. إذن ، علينا معرفة الطول أ والعرض في الشكل. ثم نطبق الصيغة P \u003d (a + b) ∙ 2. يسمى متوازي الأضلاع الذي تتساوى فيه جميع الأضلاع والزوايا بينهما المعين.

إيجاد محيط مثلث متساوي الأضلاع وقائم الزاوية

يمكن إيجاد محيط الضلع الصحيح بالصيغة P \u003d 3a ، حيث a هو طول الضلع. إذا كان غير معروف ، فيمكن العثور عليه عبر الوسيط. في المثلث القائم الزاوية ، هناك ضلعان فقط لهما نفس الأهمية. يمكن إيجاد الأساس من خلال نظرية فيثاغورس. بعد أن أصبحت قيم الأضلاع الثلاثة معروفة ، نحسب المحيط. يمكن إيجادها باستخدام الصيغة P \u003d a + b + c ، حيث a و b ضلعان متساويان ، و c هي القاعدة. تذكر أنه في المثلث المتساوي الساقين ، أ \u003d ب \u003d أ ، لذا أ + ب \u003d 2 أ ، ثم ف \u003d 2 أ + ج. على سبيل المثال ، إذا كان طول ضلع مثلث متساوي الساقين 4 سم ، فسنوجد قاعدته ومحيطه. نحسب قيمة الوتر وفقًا لنظرية فيثاغورس مع \u003d √a 2 + في 2 \u003d 16 + 16 \u003d √32 \u003d 5.65 سم ، والآن نحسب المحيط P \u003d 2 ∙ 4 + 5.65 \u003d 13.65 سم.

كيف تجد زوايا مضلع منتظم

يحدث مضلع منتظم في حياتنا كل يوم ، على سبيل المثال ، مربع عادي ، مثلث ، مثمن. يبدو أنه لا يوجد شيء أسهل من بناء هذا الرقم بنفسك. لكن هذا فقط للوهلة الأولى. من أجل بناء أي n-gon ، تحتاج إلى معرفة قيمة زواياه. لكن كيف تجدهم؟ حتى العلماء القدماء حاولوا بناء مضلعات منتظمة. لقد خمّنوا أن يكتبوها في دوائر. ثم قاموا بتمييز النقاط الضرورية عليها ، وربطوها بخطوط مستقيمة. بالنسبة للأشكال البسيطة ، تم حل مشكلة البناء. تم الحصول على الصيغ والنظريات. على سبيل المثال ، كان إقليدس في عمله الشهير "التأسيس" منخرطًا في حل المشكلات لـ 3 و 4 و 5 و 6 و 15 غون. وجد طرقًا لبنائها وإيجاد الزوايا. دعونا نرى كيف نفعل هذا لـ 15-gon. تحتاج أولاً إلى حساب مجموع زواياه الداخلية. يجب عليك استخدام الصيغة S \u003d 180⁰ (n-2). لدينا 15-gon ، وبالتالي فإن العدد n هو 15. عوض بالبيانات التي نعرفها في الصيغة ، ونحصل على S \u003d 180⁰ (15-2) \u003d 180⁰ х 13 \u003d 2340⁰. لقد أوجدنا مجموع قياسات الزوايا الداخلية لـ 15-gon. الآن أنت بحاجة إلى الحصول على قيمة كل منهم. مجموع الزوايا 15 ، أجرينا العملية الحسابية 2340⁰: 15 \u003d 156. هذا يعني أن كل زاوية داخلية هي 156 درجة ، والآن بمساعدة المسطرة والبوصلة ، يمكنك بناء 15-gon منتظم. ولكن ماذا عن n-gons الأكثر تعقيدًا؟ لقرون عديدة ، كافح العلماء لحل هذه المشكلة. تم العثور عليها فقط في القرن الثامن عشر بواسطة كارل فريدريش جاوس. كان قادرًا على بناء 65537-gon. منذ ذلك الحين ، تم اعتبار المشكلة رسميًا تم حلها بالكامل.

حساب زوايا n-gons بالراديان

بالطبع ، هناك عدة طرق للعثور على زوايا المضلعات. غالبًا ما يتم حسابها بالدرجات. ولكن يمكنك أيضًا التعبير عنها بالتقدير الدائري. كيف افعلها؟ تحتاج إلى المضي قدما على النحو التالي. أولاً ، اكتشف عدد الأضلاع مضلع منتظم، ثم نطرح 2. لذلك نحصل على القيمة: n - 2. اضرب الفرق الموجود بالرقم n ("pi" \u003d 3.14). كل ما تبقى الآن هو قسمة الناتج الناتج على عدد الزوايا في n-gon. ضع في اعتبارك هذه الحسابات باستخدام مثال نفس الشكل السداسي. إذن ، الرقم n هو 15. لنطبق الصيغة S \u003d n (n - 2): n \u003d 3.14 (15 - 2): 15 \u003d 3.14 ∙ 13: 15 \u003d 2.72. هذه بالطبع ليست الطريقة الوحيدة لحساب الزاوية بالراديان. يمكنك ببساطة قسمة الزاوية بالدرجات على 57.3. بعد كل شيء ، هذا العدد بالضبط من الدرجات يعادل راديان واحد.

حساب قيمة الزوايا بالدرجات

بالإضافة إلى الدرجات والراديان ، يمكنك محاولة إيجاد قيمة زوايا المضلع المنتظم بالدرجات. هذا يفعل كما يلي. اطرح 2 من العدد الإجمالي للزوايا ، واقسم الفرق الناتج على عدد أضلاع المضلع المنتظم. نضرب النتيجة التي تم العثور عليها في 200. بالمناسبة ، لا يتم استخدام وحدة قياس الزوايا مثل الدرجات عمليًا.

حساب الزوايا الخارجية لـ n-gons

بالنسبة لأي مضلع عادي ، يمكنك أيضًا حساب الزاوية الخارجية بالإضافة إلى المضلع الداخلي. تم العثور على معناه بنفس الطريقة كما هو الحال مع الشخصيات الأخرى. لذا ، للعثور على الركن الخارجي لمضلع منتظم ، عليك معرفة قيمة المضلع الداخلي. علاوة على ذلك ، نعلم أن مجموع هاتين الزاويتين يساوي دائمًا 180 درجة. لذلك ، نقوم بالحسابات على النحو التالي: 180 درجة ناقص قيمة الزاوية الداخلية. جد الفرق. سيكون مساويًا لقيمة الزاوية المجاورة. على سبيل المثال ، الزاوية الداخلية للمربع 90 درجة ، إذن الخارج سيكون 180 درجة - 90 درجة \u003d 90 درجة. كما نرى ، ليس من الصعب العثور عليه. يمكن أن تأخذ الزاوية الخارجية قيمة من + 180 درجة إلى -180 درجة على التوالي.

شكل تكون فيه جميع الأطراف متساوية. لذلك ، على سبيل المثال ، المثلث متساوي الأضلاع هو مضلع منتظم يتكون من ثلاثة خطوط مغلقة. في هذه الحالة ، جميع زواياه 60 درجة. جوانبها متساوية مع بعضها البعض ، لكن ليست متوازية مع بعضها البعض. المضلعات الأخرى لها نفس الخاصية ، ولكن زواياها لها قيم مختلفة. المضلعات المنتظمة الوحيدة التي لا تتساوى أضلاعها فحسب ، بل تتوازى مع بعضها البعض أيضًا هي مربع. إذا أعطيت المشكلة مثلثًا متساوي الأضلاع بمساحة u S ، فهذا غير معروف جانب يمكن العثور عليها عبر الزوايا والجوانب. بادئ ذي بدء ، أوجد ارتفاع المثلث ، h ، عموديًا على قاعدته: h \u003d a * sinα \u003d a√3 / 2 ، حيث α \u003d 60 ° هي إحدى الزوايا المجاورة لقاعدة المثلث. بناءً على هذه الاعتبارات ، قم بتحويل الصيغة لإيجاد المساحة على النحو التالي بحيث يمكن استخدامه لحساب طول الجانب: S \u003d 1 / 2a * a√3 / 2 \u003d a ^ 2 * √3 / 4 ويتبع ذلك الجانب a يساوي: a \u003d 2√S / √√3

جد ضلع رباعي الزوايا العادي باستخدام طريقة مختلفة قليلًا. إذا كان مربعًا ، فاستخدم مساحته أو قطريه كبيانات أولية: S \u003d a ^ 2 لذلك ، فإن جانب a هو: a \u003d √S بالإضافة إلى ذلك ، إذا تم إعطاء القطر ، إذن جانب يمكن حسابها باستخدام صيغة أخرى: أ \u003d د / √2

في معظم الحالات جانب صيح مضلع يمكن تحديده من خلال معرفة نصف قطر دائرة محفورة فيه أو محصورة حوله. من المعروف أن هناك علاقة بين ضلع المثلث ونصف قطر الدائرة المحصورة حول هذا الشكل: a3 \u003d R√3 ، حيث R هو نصف قطر الدائرة المحددة إذا كانت الدائرة منقوشة في مثلث ، فإن الصيغة تأخذ شكلاً مختلفًا: a3 \u003d 2r√3 ، حيث r هو نصف القطر في الشكل السداسي المنتظم ، تكون صيغة إيجاد الضلع بنصف قطر معروف للدوائر المحصورة (R) أو الدائرة المنقوشة (r) كما يلي: a6 \u003d R \u003d 2r√3 / 3 من هذه الأمثلة ، يمكننا أن نستنتج أنه لأي تعسفي n-gon معادلة البحث الأطراف في نظرة عامة يبدو كالتالي: a \u003d 2Rsin (α / 2) \u003d 2rtg (α / 2)

تشمل الأنواع الرئيسية للمضلعات مثلثًا ومتوازي أضلاع وأنواعه (معين ، مستطيل ، مربع) ، شبه منحرف ، ومضلعات منتظمة. لكل منهم طريقته الخاصة في حساب المساحة. يتم تقسيم المضلعات الأكثر تعقيدًا والمحدبة والمقعرة إلى أشكال بسيطة ، ثم يتم تلخيص مناطقها.

مضلع بنفس الأطوال من جميع الجوانب. لذلك ، مع معرفة الطول الإجمالي - المحيط - (P) والعدد الإجمالي للرؤوس أو الأضلاع (n) ، قسّم الأول على الثاني لحساب أبعاد كل حفلات (أ) الأشكال: أ \u003d P / n.

حول كل ما هو صحيح مضلع يمكن للمرء أن يصف دائرة نصف قطرها الوحيد الممكن (R) - يمكن أيضًا استخدام هذه الخاصية لحساب الطول حفلات (أ) أي مضلعإذا كان عدد الرؤوس (n) معروفًا أيضًا من الشروط. للقيام بذلك ، ضع في اعتبارك مثلث مكون من نصف قطر والجانب المطلوب. إنه مثلث متساوي الساقين يمكن إيجاد القاعدة فيه بضرب ضعف طول الجانب حفلات - نصف القطر - نصف الزاوية بينهما - الزاوية المركزية. حساب الزاوية سهل - قسّم 360 درجة على عدد الأضلاع مضلع... يجب أن تبدو الصيغة النهائية كما يلي: a \u003d 2 * R * sin (180 ° / n).

توجد خاصية مماثلة لدائرة مسجلة في مضلع محدب منتظم - إنها موجودة بالضرورة ، ويمكن أن يكون لنصف القطر قيمة فريدة لكل شكل محدد. لذلك ، هنا ، عند حساب الطول حفلات (أ) يمكن استخدام معرفة نصف القطر (r) وعدد الجوانب مضلع (ن). نصف القطر المرسوم من نقطة المماس للدائرة وأي جانب من أضلاعه متعامد على هذا الجانب ويقسمه إلى نصفين. لذلك ، ضع في اعتبارك مثلثًا قائم الزاوية يكون فيه نصف القطر ونصف القطر المرغوب حفلات أرجل. حسب التعريف ، فإن نسبتهم تساوي ظل نصف الزاوية المركزية ، والتي يمكنك حسابها بنفس الطريقة كما في الخطوة السابقة: (360 درجة / ن) / 2 \u003d 180 درجة / ن. يمكن كتابة تعريف ظل الزاوية الحادة في مثلث قائم الزاوية في هذه الحالة على النحو التالي: tg (180 ° / n) \u003d (a / 2) / r. عبر من هذه المساواة عن الطول حفلات... يجب أن تحصل على الصيغة التالية: a \u003d 2 * r * tg (180 ° / n).

يتكون المضلع من عدة مقاطع خطية متصلة ببعضها البعض وتشكل خطًا مغلقًا. جميع شخصيات هذه الفئة مقسمة إلى بسيطة ومعقدة. تتضمن المضلعات البسيطة مثلثًا ورباعي الزوايا ، وأخرى معقدة - مضلعات ذات عدد كبير حفلاتوكذلك المضلعات النجمية.

تعليمات

أكثر المشاكل التي تصادفها هي مشكلة المثلث العادي حفلاتاوه ا. نظرًا لأن المضلع منتظم ، فهو الثلاثة حفلاتق متساوية. لذلك ، بمعرفة متوسط \u200b\u200bالمثلث وارتفاعه ، يمكنك إيجاد كل ذلك حفلاتس. للقيام بذلك ، استخدم طريقة البحث حفلاتs من خلال الجيب: a \u003d x / cosα منذ ذلك الحين حفلاتإن s للمثلث متساوية ، أي a \u003d b \u003d c \u003d a، a \u003d b \u003d c \u003d x / cosα حيث x هو الارتفاع أو الوسيط أو المنصف. وبالمثل ، ابحث عن جميع المجاهيل الثلاثة حفلاتنحن في مثلث متساوي الساقين ، لكن بشرط واحد - ارتفاع معين. يجب أن يبرز على قاعدة المثلث. معرفة ارتفاع القاعدة x ، أوجد حفلاتلمثلث متساوي الساقين a: a \u003d x / cosα. بما أن a \u003d b ، بما أن المثلث متساوي الساقين ، ابحث عنه حفلاتs كما يلي: a \u003d b \u003d x / cosα بعد أن تجد الضلع حفلاتs للمثلث ، احسب طول قاعدة المثلث بتطبيق نظرية فيثاغورس لإيجاد نصف القاعدة: c / 2 \u003d √ (x / cosα) ^ 2- (x ^ 2) \u003d √x ^ 2 (1-cos ^ 2α) / cos ^ 2α \u003d xtgα ومن هنا أوجد القاعدة: c \u003d 2xtgα.

المربع عبارة عن رباعي الزوايا منتظم ، حفلاتالتي يتم حسابها بعدة طرق. تتم مناقشة كل منهم أدناه ، الطريقة الأولى تقترح البحث حفلاتs عبر قطر المربع. نظرًا لأن جميع أركان المربع صحيحة ، فإن هذا القطر يقسمهم إلى نصفين بحيث يتم تكوين مثلثين قائمين الزاوية بزاوية 45 درجة عند القاعدة. على التوالي، حفلاتوالمربع هو: a \u003d b \u003d c \u003d f \u003d d * cosα \u003d d√2 / 2 ، حيث d هو قطر المربع. إذا كان المربع محفورًا في دائرة ، فعند معرفة نصف قطر هذه الدائرة ، ابحث عنها حفلاتy: a4 \u003d R√2 ، حيث R هو نصف قطر الدائرة.

لدي الكثير حفلاتلهم المضلعات حفلاتy احسب في آخر الطرق المقترحة - عن طريق إدخال مضلع في دائرة. للقيام بذلك ، ارسم مضلعًا منتظمًا بشكل عشوائي حفلاتam ، وحولها تصف دائرة بنصف قطر معين R. تخيل أن المشكلة قد أعطيت بعض التعسفي n-gon. إذا تم وصف دائرة حول هذا مضلع، ثم لتجد حفلاتقم بتطبيق الصيغة: an \u003d 2Rsinα / 2.